문제1) 약수의 개수 구하기
숫자나라 기사단의 각 기사에게는 1번부터 number까지 번호가 지정되어 있습니다. 기사들은 무기점에서 무기를 구매하려고 합니다.
각 기사는 자신의 기사 번호의 약수 개수에 해당하는 공격력을 가진 무기를 구매하려 합니다. 단, 이웃나라와의 협약에 의해 공격력의 제한수치를 정하고, 제한수치보다 큰 공격력을 가진 무기를 구매해야 하는 기사는 협약기관에서 정한 공격력을 가지는 무기를 구매해야 합니다.
예를 들어, 15번으로 지정된 기사단원은 15의 약수가 1, 3, 5, 15로 4개 이므로, 공격력이 4인 무기를 구매합니다. 만약, 이웃나라와의 협약으로 정해진 공격력의 제한수치가 3이고 제한수치를 초과한 기사가 사용할 무기의 공격력이 2라면, 15번으로 지정된 기사단원은 무기점에서 공격력이 2인 무기를 구매합니다. 무기를 만들 때, 무기의 공격력 1당 1kg의 철이 필요합니다. 그래서 무기점에서 무기를 모두 만들기 위해 필요한 철의 무게를 미리 계산하려 합니다.
기사단원의 수를 나타내는 정수 number와 이웃나라와 협약으로 정해진 공격력의 제한수치를 나타내는 정수 limit와 제한수치를 초과한 기사가 사용할 무기의 공격력을 나타내는 정수 power가 주어졌을 때, 무기점의 주인이 무기를 모두 만들기 위해 필요한 철의 무게를 return 하는 solution 함수를 완성하시오.
제한사항
1 ≤ number ≤ 100,000
2 ≤ limit ≤ 100
1 ≤ power ≤ limit
입출력 예
| number | limit | power | result |
| 5 | 3 | 2 | 10 |
| 10 | 3 | 2 | 21 |
입출력 예 설명
입출력 예 #1
1부터 5까지의 약수의 개수는 순서대로 [1, 2, 2, 3, 2]개입니다. 모두 공격력 제한 수치인 3을 넘지 않기 때문에 필요한 철의 무게는 해당 수들의 합인 10이 됩니다. 따라서 10을 return 합니다.
입출력 예 #2
1부터 10까지의 약수의 개수는 순서대로 [1, 2, 2, 3, 2, 4, 2, 4, 3, 4]개입니다. 공격력의 제한수치가 3이기 때문에, 6, 8, 10번 기사는 공격력이 2인 무기를 구매합니다. 따라서 해당 수들의 합인 21을 return 합니다.
내가 푼 풀이)
import math
def solution(number, limit, power):
yak_list =[]
for num in range(1,number+1):
yak = 0
for i in range(1,int(math.sqrt(num))+1):
if num % i ==0:
yak +=1
if math.sqrt(num).is_integer():
yak = yak*2-1
else:
yak=yak*2
if yak > limit:
yak = power
yak_list.append(yak)
answer = sum(yak_list)
return answer
이 문제는 약수의 개수를 구하는 것이 관건인 문제입니다. 예를 들어 number가 5라고 하면 1부터 5까지의 약수의 개수를 리스트에 넣어서 계산하는 것입니다.
첫번째 예제에서 number가 5이므로 1부터 5까지 순회하는데, 이를 num이라고 두면 num=1일때의 약수는 [1]이므로 1개가 되고,
num=2일때의 약수는 [1,2]이므로 2개가 됩니다. 그리고 num=3일때는 [1,3]이 되므로 약수의 개수는 2개가 되고, num=4일때는 [1,2,4]가 되어 약수의 개수는 3개가 됩니다. 마지막으로 num=5일때는 [1,5]가 되어 약수의 개수는 2개가 됩니다.
또한 약수는 쌍으로 이뤄집니다. 또한 특정 값 n의 약수가 i라면 n / i도 약수가 됩니다. 예를 들어 특정 n의 값을 16이라고 생각했을때 약수는 (1,16),(2,8),(4,4), (8,2) (16,1) 이렇게 5개가 나옵니다. 그리고 특정 n의 값이 8이라고 했을때 약수는 (1,8),(2,4),(4,2),(8,1)로 4개가 나옵니다. 둘의 차이를 확인해보면 특정 n의 제곱근이 정수일때는 홀수개로 나오며 아닐때는 짝수개로 나오는 것을 확인할 수 있습니다.
위 내용을 보았을 때 반복문의 횟수는 n의 제곱근의 정수부분까지만 진행해도 약수를 구할 수 있다는 것을 알 수 있습니다.
위 사례로 계산해보면 n의 값이 16일때는 1~4까지만 진행하여 약수를 찾은 후 x2-1을 하면 되며 n의 값이 8일때는 1~2까지 진행 후 x2를 하면 약수의 개수가 나오게 됩니다.
시간복잡도:
이중 반복문이지만 내부 반복문은 제곱근까지만 진행하므로 시간복잡도는 O(n*n^0.5)가 됩니다.
공간복잡도:
리스트가 만들어질 공간이 필요하므로 O(n)의 공간이 필요합니다.
문제2) 에라토스테네스의 체
1부터 입력받은 숫자 n 사이에 있는 소수의 개수를 반환하는 함수, solution을 만들어 보세요.
소수는 1과 자기 자신으로만 나누어지는 수를 의미합니다.
(1은 소수가 아닙니다.)
제한 조건
n은 2이상 1000000이하의 자연수입니다.
입출력 예
| n | result |
| 10 | 4 |
| 5 | 3 |
입출력 예 설명
입출력 예 #1
1부터 10 사이의 소수는 [2,3,5,7] 4개가 존재하므로 4를 반환
입출력 예 #2
1부터 5 사이의 소수는 [2,3,5] 3개가 존재하므로 3를 반환
내가 푼 풀이)
import math
def solution(n):
sosu_list = []
for i in range(2,n+1):
for j in range(2,int(math.sqrt(i))+1):
if i % j==0:
break
else:
sosu_list.append(i)
return len(sosu_list)
시간복잡도:
문제1과 동일하게 이중 반복문이지만 내부 반복문은 제곱근까지만 진행하므로 시간복잡도는 O(n*n^0.5)가 됩니다.
공간복잡도:
리스트가 만들어질 공간이 필요하므로 O(n)의 공간이 필요합니다.
더 효율적인 풀이)
def solution(n):
sieve = [True] * (n+1) # True = 소수 후보
sieve[0], sieve[1] = False, False
for i in range(2, int(n**0.5)+1):
if sieve[i]:
# i의 배수들을 모두 제거
for j in range(i*i, n+1, i):
sieve[j] = False
return sum(sieve)
이 풀이는 에라토스테네스의 체 알고리즘을 사용한 것입니다.
이 알고리즘은 1부터 n까지의 수에서 합성수는 어떤 소수의 배수라는 성질을 이용한 것입니다.
가장 작은 소수 2부터 시작해, 그 배수들을 모두 지우고(체로 거르고), 다음으로 남아있는 수의 배수를 또 지웁니다. 끝까지 반복하면 남아있는 수들은 소수가 됩니다.
이 알고리즘의 절차는 아래와 같습니다.
첫번째, n이 주어졌다고 할 때 길이 n+1의 불리언 배열 sieve를 만들고 전부 True로 채웁니다. 그리고 sieve[0] = sieve[1] = False로 설정(0, 1은 소수가 아님)
두번째, i = 2부터 i*i <= n 까지를 반복합니다. 이때 sieve[i]가 True라면(= i가 소수라면) j를 i*i부터 n까지 i씩 증가시키며 sieve[j] = False로 설정합니다. (i의 배수들을 지움) 이때 j가 i*i부터 시작하는 이유는 i*k (k < i)는 이미 더 작은 소수들의 배수 단계에서 지워졌기 때문입니다.
마지막으로 sieve 배열에 True인 인덱스들이 소수입니다.
에라토스테네스의 체 알고리즘은 소수 판별, 개수, 목록을 구하는데 많이 사용합니다.
시간복잡도:
에라토스테네스의 체 알고리즘의 시간복잡도는 O(nlog log n)입니다. 소수들의 역수 합이 log logn 에 수렴하기 때문입니다.
공간복잡도:
불리언 배열이 하나 만들어지므로 공간복잡도는 O(n)입니다.
문제3) 페인트칠 최소횟수 - 구간 건너뛰기
어느 학교에 페인트가 칠해진 길이가 n미터인 벽이 있습니다. 벽에 동아리 · 학회 홍보나 회사 채용 공고 포스터 등을 게시하기 위해 테이프로 붙였다가 철거할 때 떼는 일이 많고 그 과정에서 페인트가 벗겨지곤 합니다. 페인트가 벗겨진 벽이 보기 흉해져 학교는 벽에 페인트를 덧칠하기로 했습니다.
넓은 벽 전체에 페인트를 새로 칠하는 대신, 구역을 나누어 일부만 페인트를 새로 칠 함으로써 예산을 아끼려 합니다. 이를 위해 벽을 1미터 길이의 구역 n개로 나누고, 각 구역에 왼쪽부터 순서대로 1번부터 n번까지 번호를 붙였습니다. 그리고 페인트를 다시 칠해야 할 구역들을 정했습니다.
벽에 페인트를 칠하는 롤러의 길이는 m미터이고, 롤러로 벽에 페인트를 한 번 칠하는 규칙은 다음과 같습니다.
롤러가 벽에서 벗어나면 안 됩니다.
구역의 일부분만 포함되도록 칠하면 안 됩니다.
즉, 롤러의 좌우측 끝을 구역의 경계선 혹은 벽의 좌우측 끝부분에 맞춘 후 롤러를 위아래로 움직이면서 벽을 칠합니다. 현재 페인트를 칠하는 구역들을 완전히 칠한 후 벽에서 롤러를 떼며, 이를 벽을 한 번 칠했다고 정의합니다.
한 구역에 페인트를 여러 번 칠해도 되고 다시 칠해야 할 구역이 아닌 곳에 페인트를 칠해도 되지만 다시 칠하기로 정한 구역은 적어도 한 번 페인트칠을 해야 합니다. 예산을 아끼기 위해 다시 칠할 구역을 정했듯 마찬가지로 롤러로 페인트칠을 하는 횟수를 최소화하려고 합니다.
정수 n, m과 다시 페인트를 칠하기로 정한 구역들의 번호가 담긴 정수 배열 section이 매개변수로 주어질 때 롤러로 페인트칠해야 하는 최소 횟수를 return 하는 solution 함수를 작성해 주세요.
제한사항
1 ≤ m ≤ n ≤ 100,000
1 ≤ section의 길이 ≤ n
1 ≤ section의 원소 ≤ n
section의 원소는 페인트를 다시 칠해야 하는 구역의 번호입니다.
section에서 같은 원소가 두 번 이상 나타나지 않습니다.
section의 원소는 오름차순으로 정렬되어 있습니다.
입출력 예
| n | m | section | result |
| 8 | 4 | [2, 3, 6] | 2 |
| 5 | 4 | [1, 3] | 1 |
| 4 | 1 | [1, 2, 3, 4] | 4 |
입출력 예 설명
입출력 예 #1
예제 1번은 2, 3, 6번 영역에 페인트를 다시 칠해야 합니다. 롤러의 길이가 4미터이므로 한 번의 페인트칠에 연속된 4개의 구역을 칠할 수 있습니다. 처음에 3, 4, 5, 6번 영역에 페인트칠을 하면 칠해야 할 곳으로 2번 구역만 남고 1, 2, 3, 4번 구역에 페인트칠을 하면 2번 만에 다시 칠해야 할 곳에 모두 페인트칠을 할 수 있습니다.

2번보다 적은 횟수로 2, 3, 6번 영역에 페인트를 덧칠하는 방법은 없습니다. 따라서 최소 횟수인 2를 return 합니다.
입출력 예 #2
예제 2번은 1, 3번 영역에 페인트를 다시 칠해야 합니다. 롤러의 길이가 4미터이므로 한 번의 페인트칠에 연속된 4개의 구역을 칠할 수 있고 1, 2, 3, 4번 영역에 페인트칠을 하면 한 번에 1, 3번 영역을 모두 칠할 수 있습니다.
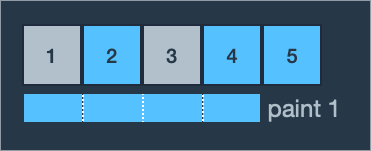
따라서 최소 횟수인 1을 return 합니다.
입출력 예 #3
예제 3번은 모든 구역에 페인트칠을 해야 합니다. 롤러의 길이가 1미터이므로 한 번에 한 구역밖에 칠할 수 없습니다. 구역이 4개이므로 각 구역을 한 번씩만 칠하는 4번이 최소 횟수가 됩니다.

따라서 4를 return 합니다.
내가 푼 풀이)
def solution(n, m, section):
answer = 0
idx = 0
while len(section) > 0:
last_num = section[0]+m-1
if last_num in section:
idx = section.index(last_num)
else:
find_num = 0
for num in section:
if num <= last_num:
find_num = num
else:
break
idx = section.index(find_num)
answer+=1
section[:idx+1] = []
return answer
시간복잡도:
외부 while문안에서 for문이 진행됩니다. m이 4라고 가정했을때 last_num보다 1작은 수가 리스트에 들어있을 경우 최악의 경우가 되며 이때 시간 복잡도는 O(n^2)이 됩니다.
공간복잡도:
section[:idx+1] = []이 계속 반복됩니다 이때 section의 idx 이후 요소들이 앞으로 이동하게 되며, 슬라이싱은 기본으로 복사를 사용하므로 추가 공간을 사용합니다. 따라서 공간복잡도는 O(n)이 됩니다.
더 효율적인 풀이)
def solution(n, m, section):
answer = 0
i = 0
while i < len(section):
# 롤러를 section[i] 위치부터 시작
paint_end = section[i] + m - 1
answer += 1
# 이 롤러 범위에 포함되는 구역들을 건너뜀
while i < len(section) and section[i] <= paint_end:
i += 1
return answer
시간복잡도:
이 풀이는 이중 while문이 사용되기는 하였지만, 인덱스 값이 section의 길이보다 작고, 세션의 인덱스에 해당하는 요소값이 paint_end보다 작거나 같으면 인덱스만 1 증가시킵니다. 따라서 내부 while문에서는 최대 len(section)만큼만 증가합니다. 그리고 외부 while문도 동일한 조건이기 때문에 반복횟수는 O(n)이 됩니다. 그런데 외부조건문이 만족하게 되면 자연스럽게 내부조건문도 만족하게 되므로 총 시간복잡도도 O(n)이 됩니다.
공간복잡도:
변수가 들어갈 추가 공간만 필요하므로 공간복잡도는 O(1)이 됩니다.
문제4) 둘만의 암호 - 문자변경
두 문자열 s와 skip, 그리고 자연수 index가 주어질 때, 다음 규칙에 따라 문자열을 만들려 합니다. 암호의 규칙은 다음과 같습니다.
문자열 s의 각 알파벳을 index만큼 뒤의 알파벳으로 바꿔줍니다.
index만큼의 뒤의 알파벳이 z를 넘어갈 경우 다시 a로 돌아갑니다.
skip에 있는 알파벳은 제외하고 건너뜁니다.
예를 들어 s = "aukks", skip = "wbqd", index = 5일 때, a에서 5만큼 뒤에 있는 알파벳은 f지만 [b, c, d, e, f]에서 'b'와 'd'는 skip에 포함되므로 세지 않습니다. 따라서 'b', 'd'를 제외하고 'a'에서 5만큼 뒤에 있는 알파벳은 [c, e, f, g, h] 순서에 의해 'h'가 됩니다. 나머지 "ukks" 또한 위 규칙대로 바꾸면 "appy"가 되며 결과는 "happy"가 됩니다.
두 문자열 s와 skip, 그리고 자연수 index가 매개변수로 주어질 때 위 규칙대로 s를 변환한 결과를 return하도록 solution 함수를 완성해주세요.
제한사항
5 ≤ s의 길이 ≤ 50
1 ≤ skip의 길이 ≤ 10
s와 skip은 알파벳 소문자로만 이루어져 있습니다.
skip에 포함되는 알파벳은 s에 포함되지 않습니다.
1 ≤ index ≤ 20
입출력 예
| s | skip | index | result |
| "aukks" | "wbqd" | 5 | "happy" |
내가 푼 풀이)
from itertools import cycle
def solution(s, skip, index):
alpabet = ['a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s','t','u','v','w','x','y','z']
answer = []
for char in s:
char_idx = alpabet.index(char)
new_str =[]
while len(new_str) <= index:
if alpabet[char_idx] not in skip:
new_str.append(alpabet[char_idx])
if char_idx+1 <= len(alpabet)-1:
char_idx+=1
else:
char_idx=0
answer.append(new_str[-1])
return ''.join(answer)
시간복잡도:
먼저 알파벳의 리스트를 만드는 시간은 O(26)이므로 O(1)이라고 볼 수 있습니다.
s문자열을 모두 순회하고 내부 반복문에서 index만큼 순회하며 skip을 순회하면서 없는지를 판단하기 때문에 걸리는 시간은
O(n*(index+len(skip)))인데 index와 skip문자열의 길이가 커진다고 생각하면 최악은 O(n^2)이 됩니다.
공간복잡도:
answer 리스트와 new_str 리스트가 만들어질 추가 공간이 필요하므로 각 O(n)이 필요합니다. 따라서 공간복잡도는 O(n)이 됩니다.
더 효율적인 풀이)
def solution(s, skip, index):
skip_set = set(skip)
answer = []
for char in s:
cnt = 0
code = ord(char)
while cnt < index:
code += 1
if code > ord('z'):
code = ord('a')
if chr(code) not in skip_set:
cnt += 1
answer.append(chr(code))
return ''.join(answer)
시간복잡도:
효율적인 풀이방법은 아스키코드를 사용하는 방법입니다. 아스키 코드를 사용하면 문자열을 숫자로 변환시킬 수 있습니다. 그리고 skip문자열을 set으로 만들어 검증 시간을 O(1)로 줄일 수 있습니다. 따라서 문자열 순회하는 시간 X index크기가 됩니다. index는 상수이므로 결국 총 시간복잡도는 O(n)이 됩니다.
공간복잡도:
answer 리스트가 생성될 공간만 필요하므로 O(n)이 됩니다.
문제5) 대충 만든 자판
휴대폰의 자판은 컴퓨터 키보드 자판과는 다르게 하나의 키에 여러 개의 문자가 할당될 수 있습니다. 키 하나에 여러 문자가 할당된 경우, 동일한 키를 연속해서 빠르게 누르면 할당된 순서대로 문자가 바뀝니다.
예를 들어, 1번 키에 "A", "B", "C" 순서대로 문자가 할당되어 있다면 1번 키를 한 번 누르면 "A", 두 번 누르면 "B", 세 번 누르면 "C"가 되는 식입니다.
같은 규칙을 적용해 아무렇게나 만든 휴대폰 자판이 있습니다. 이 휴대폰 자판은 키의 개수가 1개부터 최대 100개까지 있을 수 있으며, 특정 키를 눌렀을 때 입력되는 문자들도 무작위로 배열되어 있습니다. 또, 같은 문자가 자판 전체에 여러 번 할당된 경우도 있고, 키 하나에 같은 문자가 여러 번 할당된 경우도 있습니다. 심지어 아예 할당되지 않은 경우도 있습니다. 따라서 몇몇 문자열은 작성할 수 없을 수도 있습니다.
이 휴대폰 자판을 이용해 특정 문자열을 작성할 때, 키를 최소 몇 번 눌러야 그 문자열을 작성할 수 있는지 알아보고자 합니다.
1번 키부터 차례대로 할당된 문자들이 순서대로 담긴 문자열배열 keymap과 입력하려는 문자열들이 담긴 문자열 배열 targets가 주어질 때, 각 문자열을 작성하기 위해 키를 최소 몇 번씩 눌러야 하는지 순서대로 배열에 담아 return 하는 solution 함수를 완성해 주세요.
단, 목표 문자열을 작성할 수 없을 때는 -1을 저장합니다.
제한사항
1 ≤ keymap의 길이 ≤ 100
1 ≤ keymap의 원소의 길이 ≤ 100
keymap[i]는 i + 1번 키를 눌렀을 때 순서대로 바뀌는 문자를 의미합니다.
예를 들어 keymap[0] = "ABACD" 인 경우 1번 키를 한 번 누르면 A, 두 번 누르면 B, 세 번 누르면 A 가 됩니다.
keymap의 원소의 길이는 서로 다를 수 있습니다.
keymap의 원소는 알파벳 대문자로만 이루어져 있습니다.
1 ≤ targets의 길이 ≤ 100
1 ≤ targets의 원소의 길이 ≤ 100
targets의 원소는 알파벳 대문자로만 이루어져 있습니다.
입출력 예
| keymap | targets | result |
| ["ABACD", "BCEFD"] | ["ABCD","AABB"] | [9, 4] |
| ["AA"] | ["B"] | [-1] |
| ["AGZ", "BSSS"] | ["ASA","BGZ"] | [4, 6] |
입출력 예 설명
입출력 예 #1
"ABCD"의 경우,
1번 키 한 번 → A
2번 키 한 번 → B
2번 키 두 번 → C
1번 키 다섯 번 → D
따라서 총합인 9를 첫 번째 인덱스에 저장합니다.
"AABB"의 경우,
1번 키 한 번 → A
1번 키 한 번 → A
2번 키 한 번 → B
2번 키 한 번 → B
따라서 총합인 4를 두 번째 인덱스에 저장합니다.
결과적으로 [9,4]를 return 합니다.
입출력 예 #2
"B"의 경우, 'B'가 어디에도 존재하지 않기 때문에 -1을 첫 번째 인덱스에 저장합니다.
결과적으로 [-1]을 return 합니다.
입출력 예 #3
"ASA"의 경우,
1번 키 한 번 → A
2번 키 두 번 → S
1번 키 한 번 → A
따라서 총합인 4를 첫 번째 인덱스에 저장합니다.
"BGZ"의 경우,
2번 키 한 번 → B
1번 키 두 번 → G
1번 키 세 번 → Z
따라서 총합인 6을 두 번째 인덱스에 저장합니다.
결과적으로 [4, 6]을 return 합니다.
내가 푼 풀이)
def solution(keymap, targets):
answer = []
for target in targets:
count = 0
for char in target:
key_count = []
for key in keymap:
try:
idx = key.index(char)
key_count.append(idx+1)
except:
pass
if len(key_count) > 0:
count += min(key_count)
if len(key_count) == 0:
count = -1
break
answer.append(count)
return answer
시간복잡도:
이 풀이는 삼중 반복문안에서 실행하는데다가 index함수도 O(n)의 시간이 걸리므로 총 시간은 O(targets의 개수 x target의 길이 x keymap의 개수 x key의 길이)로 길이의 제한이 없다고 생각했을때 O(n^4)라고 할 수 있습니다.
공간복잡도:
answer 리스트가 생성될 공간이 따로 key_count 리스트가 생성될 공간이 따로 필요하므로 O(n)입니다.
더 효율적인 풀이)
def solution(keymap, targets):
# 1. 각 알파벳의 최소 입력 횟수 미리 계산
min_press = {}
for key in keymap:
for i, ch in enumerate(key):
# i+1 번 눌러야 해당 문자 입력 가능
if ch not in min_press:
min_press[ch] = i + 1
else:
min_press[ch] = min(min_press[ch], i + 1)
# 2. target 문자열 처리
answer = []
for target in targets:
total = 0
for ch in target:
if ch not in min_press: # 해당 문자가 어떤 키에도 없음
total = -1
break
total += min_press[ch]
answer.append(total)
return answer
시간복잡도:
이 풀이는 알파벳을 최소입력 횟수를 매핑하는 딕셔너리를 생성하는 이중 반복문과 타겟을 찾는 이중 반복문으로 총 2번 실행됩니다. 반복문 안에서 딕셔너리의 매핑된 값을 탐색하는 것은 O(1)의 시간이 발생하므로 시간복잡도는 O(n^2)입니다.
공간복잡도:
딕셔너리가 차지할 공간은 알파벳의 개수만큼의 공간이 필요합니다. 총 알파벳은 26개이므로 상수크기만큼의 공간만 필요합니다. 따라서 공간복잡도는 O(1)이 됩니다.
문제6) 문자열 나누기
문자열 s가 입력되었을 때 다음 규칙을 따라서 이 문자열을 여러 문자열로 분해하려고 합니다.
먼저 첫 글자를 읽습니다. 이 글자를 x라고 합시다.
이제 이 문자열을 왼쪽에서 오른쪽으로 읽어나가면서, x와 x가 아닌 다른 글자들이 나온 횟수를 각각 셉니다. 처음으로 두 횟수가 같아지는 순간 멈추고, 지금까지 읽은 문자열을 분리합니다.
s에서 분리한 문자열을 빼고 남은 부분에 대해서 이 과정을 반복합니다. 남은 부분이 없다면 종료합니다.
만약 두 횟수가 다른 상태에서 더 이상 읽을 글자가 없다면, 역시 지금까지 읽은 문자열을 분리하고, 종료합니다.
문자열 s가 매개변수로 주어질 때, 위 과정과 같이 문자열들로 분해하고, 분해한 문자열의 개수를 return 하는 함수 solution을 완성하세요.
제한사항
1 ≤ s의 길이 ≤ 10,000
s는 영어 소문자로만 이루어져 있습니다.
입출력 예
| s | result |
| "banana" | 3 |
| "abracadabra" | 6 |
| "aaabbaccccabba" | 3 |
입출력 예 설명
입출력 예 #1
s="banana"인 경우 ba - na - na와 같이 분해됩니다.
입출력 예 #2
s="abracadabra"인 경우 ab - ra - ca - da - br - a와 같이 분해됩니다.
입출력 예 #3
s="aaabbaccccabba"인 경우 aaabbacc - ccab - ba와 같이 분해됩니다.
내가 푼 풀이)
def solution(s):
answer = []
first = None
outer = []
inner = []
for char in s:
if not first:
first = char
inner.append(char)
outer.append(char)
else:
if char == first:
inner.append(char)
outer.append(char)
else:
outer.append(char)
if len(outer) == len(inner) * 2:
answer.append(''.join(outer))
first = None
inner = []
outer = []
if len(outer) > 0:
answer.append(''.join(outer))
return len(answer)
시간복잡도:
이 풀이에서는 반복문안에서 문자열을 분해할때 answer리스트안에 outer 배열의 값을 문자열로 만드는 과정이 있습니다. 문자열 생성에는 O(n)이 걸리고 반복문도 O(n)이 걸리므로 시간복잡도는 최악의 경우 O(n)이 될 수 있습니다.
공간복잡도:
answer, outer, inner 각 리스트가 생성될 공간이 필요하고 answer 리스트안에서는 문자열이 생성될 공간도 필요하므로 최악의 경우 공간복잡도는 O(n^2)이 될 수 있습니다.
더 효율적인 풀이)
def solution(s):
answer = 0
first = None
same = 0
diff = 0
for ch in s:
if first is None:
first = ch
same = 1
diff = 0
else:
if ch == first:
same += 1
else:
diff += 1
if same == diff:
answer += 1
first = None
same = diff = 0
if first is not None: # 남은 문자열 처리
answer += 1
return answer
시간복잡도:
이 풀이에서는 리스트에 들어갈 값은 고려하지 않고 리스트 요소의 개수만 계산하는 방법입니다. 따라서 문자열 반복에 대한 시간복잡도만 계산하면 됩니다. 이는 O(n)이므로 총 시간복잡도는 O(n)이 됩니다.
공간복잡도:
리스트를 생성하지않고 변수들이 저장될 공간만 추가로 필요하므로 공간복잡도는 O(1)입니다.
문제7) 데이터 분석
AI 엔지니어인 현식이는 데이터를 분석하는 작업을 진행하고 있습니다. 데이터는 ["코드 번호(code)", "제조일(date)", "최대 수량(maximum)", "현재 수량(remain)"]으로 구성되어 있으며 현식이는 이 데이터들 중 조건을 만족하는 데이터만 뽑아서 정렬하려 합니다.
예를 들어 다음과 같이 데이터가 주어진다면
data = [[1, 20300104, 100, 80], [2, 20300804, 847, 37], [3, 20300401, 10, 8]]
이 데이터는 다음 표처럼 나타낼 수 있습니다.
code date maximum remain
1 20300104 100 80
2 20300804 847 37
3 20300401 10 8
주어진 데이터 중 "제조일이 20300501 이전인 물건들을 현재 수량이 적은 순서"로 정렬해야 한다면 조건에 맞게 가공된 데이터는 다음과 같습니다.
data = [[3,20300401,10,8],[1,20300104,100,80]]
정렬한 데이터들이 담긴 이차원 정수 리스트 data와 어떤 정보를 기준으로 데이터를 뽑아낼지를 의미하는 문자열 ext, 뽑아낼 정보의 기준값을 나타내는 정수 val_ext, 정보를 정렬할 기준이 되는 문자열 sort_by가 주어집니다.
data에서 ext 값이 val_ext보다 작은 데이터만 뽑은 후, sort_by에 해당하는 값을 기준으로 오름차순으로 정렬하여 return 하도록 solution 함수를 완성해 주세요. 단, 조건을 만족하는 데이터는 항상 한 개 이상 존재합니다.
제한사항
1 ≤ data의 길이 ≤ 500
data[i]의 원소는 [코드 번호(code), 제조일(date), 최대 수량(maximum), 현재 수량(remain)] 형태입니다.
1 ≤ 코드 번호≤ 100,000
20000101 ≤ 제조일≤ 29991231
data[i][1]은 yyyymmdd 형태의 값을 가지며, 올바른 날짜만 주어집니다. (yyyy : 연도, mm : 월, dd : 일)
1 ≤ 최대 수량≤ 10,000
1 ≤ 현재 수량≤ 최대 수량
ext와 sort_by의 값은 다음 중 한 가지를 가집니다.
"code", "date", "maximum", "remain"
순서대로 코드 번호, 제조일, 최대 수량, 현재 수량을 의미합니다.
val_ext는 ext에 따라 올바른 범위의 숫자로 주어집니다.
정렬 기준에 해당하는 값이 서로 같은 경우는 없습니다.
입출력 예
| data | ext | val_ext | sort_by | result |
| [[1, 20300104, 100, 80], [2, 20300804, 847, 37], [3, 20300401, 10, 8]] | "date" | 20300501 | "remain" | [[3,20300401,10,8],[1,20300104,100,80]] |
내가 푼 풀이)
def solution(data, ext, val_ext, sort_by):
new_data = []
for d in data:
new_data.append(dict(
code=d[0],
date=d[1],
maximum=d[2],
remain=d[3]
))
new_data2 = []
for d in new_data:
if d.get(ext) < val_ext:
new_data2.append(d)
new_data2.sort(key=lambda d: d.get(sort_by))
answer = []
for d in new_data2:
answer.append([
d.get('code'),
d.get('date'),
d.get('maximum'),
d.get('remain')
])
return answer
시간복잡도:
이 풀이에서는 이중반복문의 내부를 딕셔너리로 변환해서 풀이했습니다. 딕셔너리로 변환 후 조회시에는 O(1)의 시간이 걸리므로 적게 걸릴 것이라 생각했기 때문입니다. 그리고 빅오표기법의 시간복잡도는 반복문이 3번 반복되어 각 O(n)의 시간이 걸리고 정렬을 한번 하므로 n(log n)의 시간 복잡도가 발생하여 총 시간복잡도는 O(nlog n)입니다.
공간복잡도:
리스트가 들어갈 공간들이 필요하므로 O(n)의 공간복잡도를 가집니다.
더 효율적인 풀이)
def solution(data, ext, val_ext, sort_by):
# 컬럼 이름 → 인덱스 매핑
idx_map = {
"code": 0,
"date": 1,
"maximum": 2,
"remain": 3
}
ext_idx = idx_map[ext]
sort_idx = idx_map[sort_by]
# 조건 만족하는 데이터 필터링
filtered = [row for row in data if row[ext_idx] < val_ext]
# sort_by 기준으로 정렬
filtered.sort(key=lambda x: x[sort_idx])
return filtered
시간복잡도:
이 풀이에서는 이중 반복문의 키 값과 인덱스를 매칭하는 방법입니다. 내가 푼 풀이에서는 딕셔너리 생성에 4번의 시간만 필요합니다. 그러나 반복문안에서 실행되기 때문에 매 순환마다 4번의 시간이 발생하여 반복문이 모두 실행되는데에는 상당한 시간이 소요 됩니다. 그러나 이 풀이에서는 키와 인덱스로 딕셔너리를 만든 후 인덱스를 매핑하는 방법을 사용했기에 추가 데이터를 생성하는 시간이 없어 훨씬 적은 시간이 소요됩니다. 게다가 내가 푼 풀이에서는 만든 딕셔너리를 다시 리스트 변환하는 작업이 필요하지만 이 풀이에서는 변환에 발생하는 시간이 없습니다. 따라서 시간복잡도는 같은 O(nlog n)이지만 훨씬 효율적입니다.
공간복잡도:
필터링된 데이터만 저장할 추가공간이 필요하므로 O(n)입니다.
문제8) 햄버거 만들기
햄버거 가게에서 일을 하는 상수는 햄버거를 포장하는 일을 합니다. 함께 일을 하는 다른 직원들이 햄버거에 들어갈 재료를 조리해 주면 조리된 순서대로 상수의 앞에 아래서부터 위로 쌓이게 되고, 상수는 순서에 맞게 쌓여서 완성된 햄버거를 따로 옮겨 포장을 하게 됩니다. 상수가 일하는 가게는 정해진 순서(아래서부터, 빵 – 야채 – 고기 - 빵)로 쌓인 햄버거만 포장을 합니다. 상수는 손이 굉장히 빠르기 때문에 상수가 포장하는 동안 속 재료가 추가적으로 들어오는 일은 없으며, 재료의 높이는 무시하여 재료가 높이 쌓여서 일이 힘들어지는 경우는 없습니다.
예를 들어, 상수의 앞에 쌓이는 재료의 순서가 [야채, 빵, 빵, 야채, 고기, 빵, 야채, 고기, 빵]일 때, 상수는 여섯 번째 재료가 쌓였을 때, 세 번째 재료부터 여섯 번째 재료를 이용하여 햄버거를 포장하고, 아홉 번째 재료가 쌓였을 때, 두 번째 재료와 일곱 번째 재료부터 아홉 번째 재료를 이용하여 햄버거를 포장합니다. 즉, 2개의 햄버거를 포장하게 됩니다.
상수에게 전해지는 재료의 정보를 나타내는 정수 배열 ingredient가 주어졌을 때, 상수가 포장하는 햄버거의 개수를 return 하도록 solution 함수를 완성하시오.
제한사항
1 ≤ ingredient의 길이 ≤ 1,000,000
ingredient의 원소는 1, 2, 3 중 하나의 값이며, 순서대로 빵, 야채, 고기를 의미합니다.
입출력 예
| ingredient | result |
| [2, 1, 1, 2, 3, 1, 2, 3, 1] | 2 |
| [1, 3, 2, 1, 2, 1, 3, 1, 2] | 0 |
풀이)
def solution(ingredient):
stack = []
count = 0
for item in ingredient:
stack.append(item)
# 스택 마지막 4개가 햄버거 패턴인지 확인
if stack[-4:] == [1, 2, 3, 1]:
# 햄버거 완성 → 재료 제거
del stack[-4:]
count += 1
return count
시간복잡도:
이 풀이는 새로운 리스트를 만들어 데이터를 넣어가면서 마지막 4자리가 1,2,3,1이 만들어질때마다 제거하는 방법입니다.
중간을 제거하고 데이터를 넣으면 실제로 마지막 4자리는 제거된 인덱스의 -3부분부터 마지막자리까지 확인하게 되므로
인덱스를 지정해줄 필요가 없습니다. 또한 이 방법은 ingredient 리스트를 한번만 순회하므로 시간복잡도는 O(n)입니다.
이 문제는 범위가 매우 크기 때문에 시간 복잡도가 O(n)보다 더 많이 걸린다면 시간초과가 발생할 수 있으므로 stack을 이용한 풀이가 적합합니다.
공간복잡도:
스택 리스트가 생성될 공간만 필요하므로 O(n)입니다.
문제9) 숫자 짝꿍
두 정수 X, Y의 임의의 자리에서 공통으로 나타나는 정수 k(0 ≤ k ≤ 9)들을 이용하여 만들 수 있는 가장 큰 정수를 두 수의 짝꿍이라 합니다(단, 공통으로 나타나는 정수 중 서로 짝지을 수 있는 숫자만 사용합니다). X, Y의 짝꿍이 존재하지 않으면, 짝꿍은 -1입니다. X, Y의 짝꿍이 0으로만 구성되어 있다면, 짝꿍은 0입니다.
예를 들어, X = 3403이고 Y = 13203이라면, X와 Y의 짝꿍은 X와 Y에서 공통으로 나타나는 3, 0, 3으로 만들 수 있는 가장 큰 정수인 330입니다. 다른 예시로 X = 5525이고 Y = 1255이면 X와 Y의 짝꿍은 X와 Y에서 공통으로 나타나는 2, 5, 5로 만들 수 있는 가장 큰 정수인 552입니다(X에는 5가 3개, Y에는 5가 2개 나타나므로 남는 5 한 개는 짝 지을 수 없습니다.)
두 정수 X, Y가 주어졌을 때, X, Y의 짝꿍을 return하는 solution 함수를 완성해주세요.
제한사항
3 ≤ X, Y의 길이(자릿수) ≤ 3,000,000입니다.
X, Y는 0으로 시작하지 않습니다.
X, Y의 짝꿍은 상당히 큰 정수일 수 있으므로, 문자열로 반환합니다.
입출력 예
| X | Y | result |
| "100" | "2345" | "-1" |
| "100" | "203045" | "0" |
| "100" | "123450" | "10" |
| "12321" | "42531" | "321" |
| "5525" | "1255" | "552" |
입출력 예 설명
입출력 예 #1
X, Y의 짝꿍은 존재하지 않습니다. 따라서 "-1"을 return합니다.
입출력 예 #2
X, Y의 공통된 숫자는 0으로만 구성되어 있기 때문에, 두 수의 짝꿍은 정수 0입니다. 따라서 "0"을 return합니다.
입출력 예 #3
X, Y의 짝꿍은 10이므로, "10"을 return합니다.
입출력 예 #4
X, Y의 짝꿍은 321입니다. 따라서 "321"을 return합니다.
내가 푼 풀이)
from collections import Counter
def solution(X, Y):
answer_list = []
common = Counter(X) & Counter(Y)
for key in common:
for _ in range(common.get(key)):
answer_list.append(key)
if len(answer_list) == 0:
return '-1'
answer_list.sort(reverse=True)
answer = ''.join(answer_list)
if answer == '0'*len(answer_list):
return '0'
return answer
시간복잡도:
X,Y를 리스트로 만들어 각각을 정렬해서 풀이도 해봤지만 시간초과가 발생했습니다. 그래서 collections의 Counter함수를 사용했습니다. Counter함수는 문자열에서 각 문자를 key로 하며 문자의 개수를 value로 반환하여 Counter타입으로 만들어주는 함수입니다. 그런데 Counter 타입에서는 &연산자를 사용하면 집합의 교집합과 비슷한 효과를 볼 수 있습니다. 따라서 Counter(X) & Counter(Y)를 하게되면 공통된 문자와 개수를 알 수 있습니다. 그리고 Counter 함수의 시간복잡도는 각 O(n)이 되며 &연산자는 key의 개수만큼 순회합니다. 이때 숫자는 0~9까지 이므로 O(1)이라고 볼 수 있습니다.
따라서 총 시간복잡도는 O(len(X)+len(Y)+n log n)이라서 O(nlog n)입니다. 그러나 여기서 n은 두개의 교집합의 개수이므로 매우 작다고 볼 수 있습니다.
공간복잡도:
answer_list가 생성될 공간이 필요하므로 O(n)이 됩니다. 마찬가지로 여기서도 n은 두개의 교집합의 개수입니다.
더 효율적인 풀이)
from collections import Counter
def solution(X, Y):
counter_X = Counter(X)
counter_Y = Counter(Y)
answer = []
# 9~0 순서로 최대한 많이 선택
for digit in map(str, range(9, -1, -1)):
count = min(counter_X.get(digit, 0), counter_Y.get(digit, 0))
answer.extend([digit] * count)
if not answer:
return '-1'
if answer[0] == '0': # 모든 숫자가 0 -> 내림차순 정렬이 되어있으므로 첫번째값이 0이면 나머지도 0
return '0'
return ''.join(answer)
시간복잡도:
내가 푼 풀이와 동일하게 Counter함수로 Counter를 생성하는데는 각 O(n)시간이 발생합니다.
그리고 9~0까지 거꾸로 순회하면서 counter 두개를 비교하여 값이 작은 값의 개수만큼 문자를 answer 리스트에 추가합니다. 이렇게하여 교집합 효과를 발생시킵니다. 당연히 9번만 순회하므로 O(1)이 됩니다. 이 풀이가 더 효율적인 이유는 정렬을 하지않아 시간복잡도가 O(n)이라는 것이기 때문입니다.
공간복잡도:
answer 리스트가 생성될 공간이 필요하므로 O(n)이 됩니다.
'Tools & Functions > 코딩 테스트 복기' 카테고리의 다른 글
| 프로그래머스 level0 파이썬 복기 -3 (2) | 2025.08.26 |
|---|---|
| 프로그래머스 level0 파이썬 복기 -2 (5) | 2025.08.26 |
| 프로그래머스 level0 자바 복기 (0) | 2025.08.24 |
| 프로그래머스 level0 파이썬 복기 -1 (0) | 2024.05.19 |

