1. 이진트리
이진트리는 말그대로 나무형태를 가진 자료구조입니다.

위 그림에서 가장 맨위에 있는 빨간 공이 root노드가 됩니다. 그리고 각 이진트리에서 각 노드는 최대 2개의 자식 노드를 가질 수 있습니다. 노드들 중 자식이 없는 노드는 leaf노드라고 합니다. 그리고 root로부터 leaf까지의 거리를 높이라고 합니다.
트리의 구조를 파이썬과 자바의 코드로 확인해보겠습니다.
파이썬
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def preorder(node): # root를 가장 먼저 출력 후 왼쪽으로 가면서 먼저 출력 -> 1단계씩 올라가면서 오른쪽 출력 후 root의 오른쪽으로 이동
if node:
print(node.value, end=' ')
preorder(node.left)
preorder(node.right)
def inorder(node): # 가장 왼쪽의 마지막 자식 노드부터 출력 후 1단계씩 올라가면서 오른쪽 노드를 출력 -> root의 왼쪽 노드가 모두 출력되었다면 root 출력 후 오른쪽 자식으로 이동
if node:
inorder(node.left)
print(node.value, end=' ')
inorder(node.right)
def postorder(node): # 마지막 자식 노드의 왼쪽 오른쪽 순으로 출력 후 가장 마지막에 root 노드를 출력
if node:
postorder(node.left)
postorder(node.right)
print(node.value, end=' ')
from collections import deque # deque 내장 라이브러리
def levelorder(node): # 트리의 위에서부터 아래방향으로 순회하도록 하는 방식
if not node:
return
queue = deque([node])
while queue:
current = queue.popleft()
print(current.value, end=' ')
# Current Node
if current.left:
queue.append(current.left)
if current.right:
queue.append(current.right)
root = Node(1) # root 노드 생성
root.left = Node(2) # root노드의 왼쪽 자식에 노드를 생성
root.right = Node(3) # root노드의 오른쪽 자식에 노드를 생성
root.left.left = Node(4) # root노드의 왼쪽 자식의 왼쪽 자식에 노드를 생성
root.left.right = Node(5) # root노드의 왼쪽 자식의 오른쪽 자식에 노드를 생성
root.right.left = Node(6) # root노드의 오른쪽 자식의 왼쪽 자식에 노드를 생성
root.right.right = Node(7) # root노드의 오른쪽 자식의 오른쪽 자식에 노드를 생성
# 출력값으로 순서 확인 가능
print("Preorder:")
preorder(root) # 1 2 4 5 3 6 7
print("\nInorder:")
inorder(root) # 4 2 5 1 6 3 7
print("\nPostorder:")
postorder(root) # 4 5 2 6 7 3 1
print("\nLevelorder:")
levelorder(root) # 1 2 3 4 5 6 7
자바
import java.util.*;
class Node {
int value;
Node left, right;
Node(int val) {
value = val;
left = right = null;
}
}
public class BinaryTreeTraversal {
static void preorder(Node node) { // root를 가장 먼저 출력 후 왼쪽으로 가면서 먼저 출력 -> 1단계씩 올라가면서 오른쪽 출력 후 root의 오른쪽으로 이동
if (node != null) {
System.out.print(node.value + " ");
preorder(node.left);
preorder(node.right);
}
}
static void inorder(Node node) { // 가장 왼쪽의 마지막 자식 노드부터 출력 후 1단계씩 올라가면서 오른쪽 노드를 출력 -> root의 왼쪽 노드가 모두 출력되었다면 root 출력 후 오른쪽 자식으로 이동
if (node != null) {
inorder(node.left);
System.out.print(node.value + " ");
inorder(node.right);
}
}
static void postorder(Node node) { // 마지막 자식 노드의 왼쪽 오른쪽 순으로 출력 후 가장 마지막에 root 노드를 출력
if (node != null) {
postorder(node.left);
postorder(node.right);
System.out.print(node.value + " ");
}
}
static void levelorder(Node node) { // 트리의 위에서부터 아래방향으로 순회하도록 하는 방식
if (node == null) return;
Queue<Node> queue = new LinkedList<>();
queue.offer(node);
while (!queue.isEmpty()) {
Node current = queue.poll();
System.out.print(current.value + " ");
// Current Node
if (current.left != null) {
queue.offer(current.left);
}
if (current.right != null) {
queue.offer(current.right);
}
}
}
public static void main(String[] args) {
Node root = new Node(1); // root 노드 생성
root.left = new Node(2); // root노드 자식의 왼쪽부분에 노드를 생성
root.right = new Node(3); // root노드 자식의 오른쪽부분에 노드를 생성
root.left.left = new Node(4); // root노드 왼쪽 자식의 왼쪽자식에 노드를 생성
root.left.right = new Node(5); //root노드 왼쪽 자식의 오른쪽 자식에 노드를 생성
root.right.left = new Node(6); // root노드 오른쪽 자식의 왼쪽자식에 노드를 생성
root.right.right = new Node(7); //root노드 오르쪽 자식의 오른쪽 자식에 노드를 생성
// 출력결과로 순서 확인 가능
System.out.println("Preorder:");
preorder(root); // 1 2 4 5 3 6 7
System.out.println("\nInorder:");
inorder(root); // 4 2 5 1 6 3 7
System.out.println("\nPostorder:");
postorder(root); // 4 5 2 6 7 3 1
System.out.println("\nLevelorder:");
levelorder(root); // 1 2 3 4 5 6 7
}
}
위 코드에서 4가지 순회방식을 소개하였습니다. 이 순회방식은 각각 적합한 용도가 있습니다.
먼저 preorder는 루트를 먼저 방문하므로 트리구조를 복제하거나 저장할때 유용합니다. inorder는 오름차순으로 정렬된 결과를 얻을때 사용됩니다. postorder는 하위노드부터 삭제가 필요한 상황이나 트리전체를 삭제할 필요가 있을때 사용합니다.
마지막으로 levelorder는 최단경로 탐색이나 트리를 깊이별로 순회할 필요가 있을때 사용됩니다.
2. 이진탐색트리
이진탐색트리는 이진트리에서 조건이 더 하나 붙은 자료구조입니다. 그 조건은 각 노드의 값은 왼쪽 자식이 가진 값보다는 크고 오른쪽 자식의 값보다는 작아야 한다는 것입니다. 따라서 트리의 leaf에서도 가장 왼쪽의 leaf 값이 가장 작고 가장 오른쪽의 leaf값이 가장 크게됩니다. 그리고 자식노드로 내려가더라도 부모노드에서 왼쪽은 부모노드값보다 작고, 부모노드에서 오른쪽은 부모노드보다 크게 됩니다.
이를 그림으로 표현하면 아래와 같습니다.
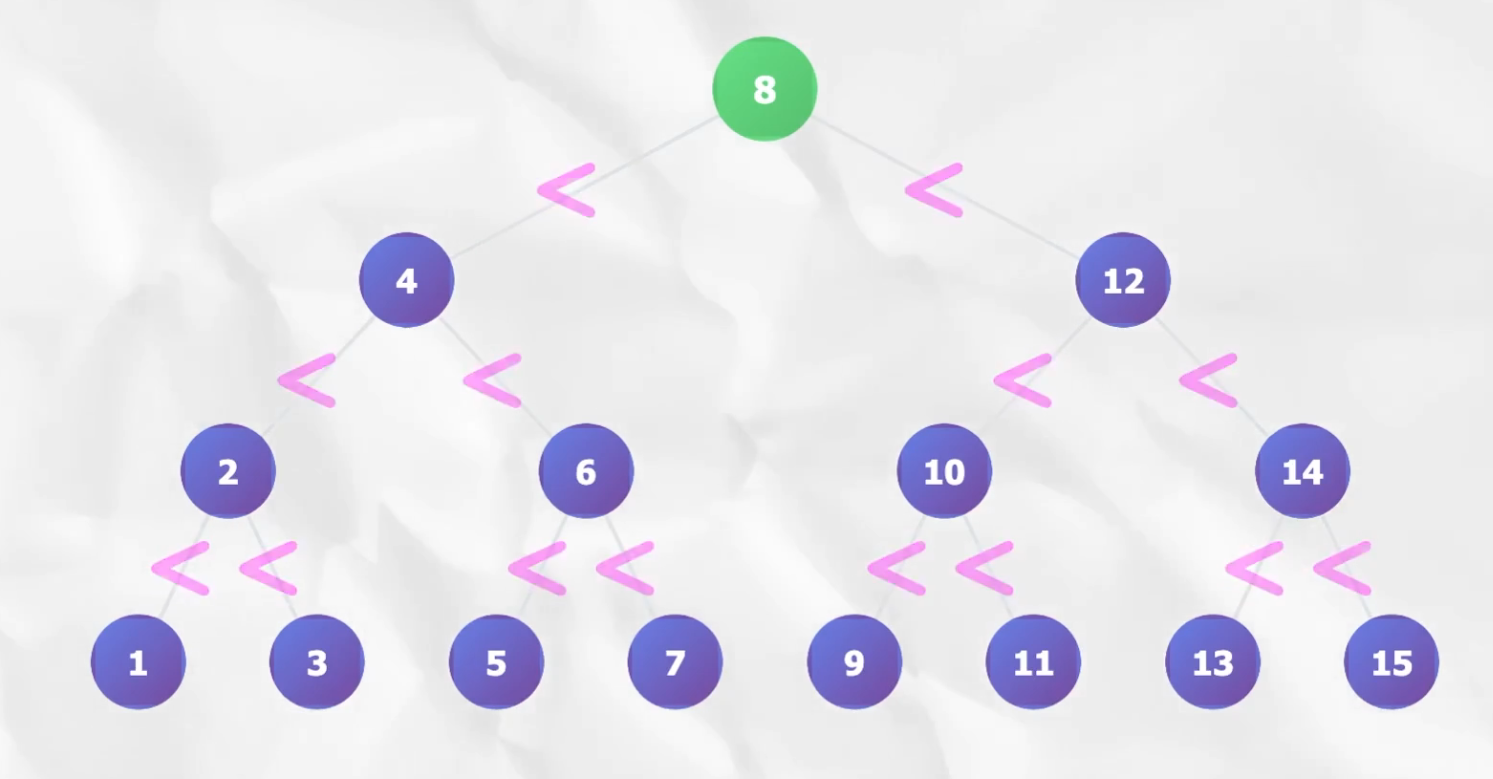
이진탐색트리는 삽입, 탐색, 제거가 모두 평균 log n의 시간복잡도를 가집니다.
탐색이 log n인 이유는 root에서 시작 후 원하는 값과 비교하여 root값보다 작다면 왼쪽 자식으로 크다면 오른쪽 자식으로 이동합니다. 그리고 자식 노드와 크기를 비교하여 작다면 왼쪽 자식으로 크다면 오른쪽 자식으로 이동합니다. 이러한 방법은 자료가 증가해도 동일한 비율보다는 작게 시간이 증가합니다. 왜냐하면 자식 노드는 부모노드의 2배씩 증가하는 반면 탐색 시간은 높이만큼만 증가할 것이기 때문입니다.
또한 삽입과 삭제도 탐색 후 자료를 추가하는 것이기 때문에 동일하게 log n의 시간복잡도를 가집니다.
이진 탐색트리에서 삽입방식은 root노드부터 시작하여 삽입할 값을 비교한 후 작다면 왼쪽 자식으로 크다면 오른쪽 자식으로 이동하는 탐색 반복 후 값을 추가합니다. 따라서 탐색 시간이 곧 삽입시간이기 때문에 log n입니다.
삭제 방식은 삭제할 값을 탐색하여 찾은 후 그 값보다 큰 값들 중 가장 작은 값을 찾아 원하는 값이 있던 노드에 삽입합니다. 그리고 값을 삭제하는 것입니다. 따라서 삭제할 값을 탐색하는 시간 + 삭제할 값보다 큰 값 중 가장 작은 값을 탐색하는 시간이 됩니다. 그러나 이것또한 빅오표기법상 log n이 됩니다.
이진 탐색트리를 파이썬과 자바코드로 확인해보겠습니다.
파이썬
class Node:
def __init__(self, val):
self.value = val
self.left = None
self.right = None
class BST:
def insert(self, node, val):
if not node:
return Node(val) # 루트 노드 삽입
if val < node.value:
node.left = self.insert(node.left, val) # 재귀함수 사용
elif val > node.value:
node.right = self.insert(node.right, val)
return node
def search(self, node, val):
if not node or node.value == val:
return node
if val < node.value:
return self.search(node.left, val)
else:
return self.search(node.right, val)
# 가장 작은 값을 찾는 메서드
def minValueNode(self, node):
current = node
while current.left:
current = current.left
return current
def delete(self, node, val):
if not node:
return node
if val < node.value:
node.left = self.delete(node.left, val)
elif val > node.value:
node.right = self.delete(node.right, val)
else:
if not node.left:
return node.right
elif not node.right:
return node.left
temp = self.minValueNode(node.right)
node.value = temp.value
node.right = self.delete(node.right, temp.value)
return node
def inorder(self, node):
if node:
self.inorder(node.left)
print(node.value, end=' ')
self.inorder(node.right)
tree = BST()
root = None
for val in [50, 30, 70, 20, 40, 60, 80]:
root = tree.insert(root, val)
print("Inorder before deletion:")
tree.inorder(root)
# 20 30 40 50 60 70 80
root = tree.delete(root, 30)
print("\nInorder after deleting 50:")
tree.inorder(root)
# 20 40 50 60 70 80
print("\nSearch 70:")
print(tree.search(root, 70).value)
#70
자바
class Node {
int value;
Node left, right;
Node(int val) {
value = val;
left = right = null;
}
}
public class BST {
Node insert(Node node, int val) {
if (node == null) return new Node(val);
if (val < node.value)
node.left = insert(node.left, val);
else if (val > node.value)
node.right = insert(node.right, val);
return node;
}
Node search(Node node, int val) {
if (node == null || node.value == val) return node;
if (val < node.value)
return search(node.left, val);
else
return search(node.right, val);
}
Node minValueNode(Node node) {
while (node.left != null)
node = node.left;
return node;
}
Node delete(Node node, int val) {
if (node == null) return node;
if (val < node.value)
node.left = delete(node.left, val);
else if (val > node.value)
node.right = delete(node.right, val);
else {
if (node.left == null) return node.right;
if (node.right == null) return node.left;
Node temp = minValueNode(node.right);
node.value = temp.value;
node.right = delete(node.right, temp.value);
}
return node;
}
void inorder(Node node) {
if (node != null) {
inorder(node.left);
System.out.print(node.value + " ");
inorder(node.right);
}
}
public static void main(String[] args) {
BST tree = new BST();
Node root = null;
int[] values = {50, 30, 70, 20, 40, 60, 80};
for (int val : values)
root = tree.insert(root, val);
System.out.println("Inorder before deletion:");
tree.inorder(root);
// 20 30 40 50 60 70 80
root = tree.delete(root, 30);
System.out.println("\nInorder after deleting 50:");
tree.inorder(root);
// 20 40 50 60 70 80
System.out.println("Search 70:");
System.out.println(tree.search(root, 70).value);
// 70
}
}3. AVL 트리
위에서 설명한 이진트리의 단점으로는 정렬된 데이터가 삽입될 경우 한쪽 노드로만 치우치게 삽입되어 시간복잡도가 O(n)이 된다는 것입니다. 이를 해결하기 위해 고안된 것이 AVL트리입니다.
AVL 트리는 트리에 불균형이 발생할때마다 노드의 배치를 조정하여 균형을 유지해주는 트리입니다.
트리에 값을 넣거나 빼는 과정에서 한쪽이 다른쪽보다 두 레벨이상 크거나 작으면 노드들을 옮겨 균형을 맞추는 것입니다.
이 트리에서는 균형을 맞추기 위해 회전이라는 개념을 사용합니다. 회전이란 트리를 이동시켜 균형을 맞추는 작업입니다.
예를 들면 3 -> 2 -> 1 순으로 요소가 삽입된다고 가정해보겠습니다.

이진 탐색 트리라면 위 그림처럼 트리가 만들어질 것입니다. 이것을 균형있게 맞추려면 2가 부모노드로 이동하고 1은 왼쪽 자식, 3은 오른쪽 자식 노드가 되어야 합니다.

그러면 위 그림처럼 균형이 만들어집니다. 왼쪽 자식의 왼쪽 자식에 의해 불균형이 발생했기 때문에 LL회전이라고 합니다.
반대로 1 -> 2 -> 3 순으로 요소를 삽입한다면 오른쪽 자식의 오른쪽 자식에 의해 불균형이 발생하게 됩니다. 따라서 RR 회전을 해서 균형을 맞출 수 있습니다.
이번에는 3 -> 1 -> 2로 요소를 삽입해보겠습니다.

위와 같은 구조로 만들어질것입니다. 그런데 이것은 왼쪽 자식의 오른쪽 자식때문에 불균형이 발생합니다. 이를 해결하기 위한 회전은 2단계로 해야합니다. 먼저 정렬을 맞추기 위해 2의 값을 1값의 노드로 이동하고 왼쪽 자식 노드를 만들어 1을 삽입합니다. 그리고 원래 2가 있던 노드는 제거합니다. 그러면 아래 그림처럼 만들어집니다.

그리고 나서 LL회전을 시키면 아래 그림처럼 균형을 맞출 수 있게됩니다.
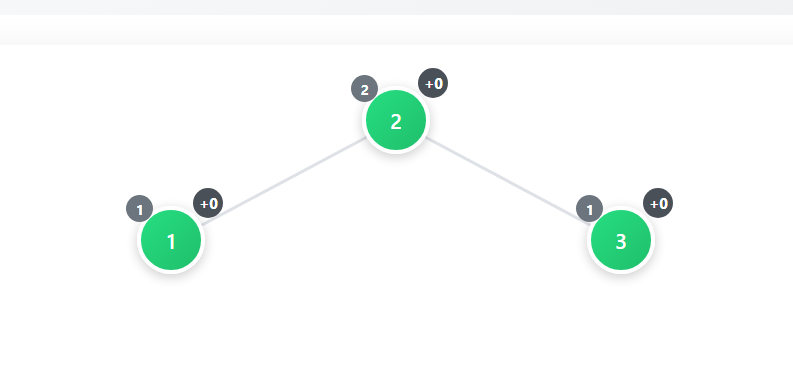
이 회전은 왼쪽 노드의 오른쪽 자식때문에 발생했기 때문에 LR회전이라고 합니다.
같은 원리로 오른쪽 자식의 왼쪽 자식때문에 불균형이 발생한다면 RL회전이라고 합니다.
이 트리를 파이썬과 자바코드로 확인해보겠습니다.
파이썬
class Node:
def __init__(self, val):
self.value = val
self.left = None
self.right = None
self.height = 1
class AVL:
def getHeight(self, node):
return node.height if node else 0
def getBalance(self, node):
return (self.getHeight(node.left) -
self.getHeight(node.right)) if node else 0
def rotateRight(self, y):
x = y.left
T2 = x.right
x.right = y
y.left = T2
y.height = 1 + max(self.getHeight(y.left),
self.getHeight(y.right))
x.height = 1 + max(self.getHeight(x.left),
self.getHeight(x.right))
return x
def rotateLeft(self, x):
y = x.right
T2 = y.left
y.left = x
x.right = T2
x.height = 1 + max(self.getHeight(x.left),
self.getHeight(x.right))
y.height = 1 + max(self.getHeight(y.left),
self.getHeight(y.right))
return y
def insert(self, node, val):
if not node:
return Node(val)
if val < node.value:
node.left = self.insert(node.left, val)
elif val > node.value:
node.right = self.insert(node.right, val)
else:
return node # duplicate not allowed
node.height = 1 + max(self.getHeight(node.left),
self.getHeight(node.right))
balance = self.getBalance(node)
if balance > 1:
if val < node.left.value: # LL
return self.rotateRight(node)
else: # LR
node.left = self.rotateLeft(node.left)
return self.rotateRight(node)
if balance < -1:
if val > node.right.value: # RR
return self.rotateLeft(node)
else: # RL
node.right = self.rotateRight(node.right)
return self.rotateLeft(node)
return node
def minValueNode(self, node):
while node.left:
node = node.left
return node
def delete(self, node, val):
if not node:
return node
if val < node.value:
node.left = self.delete(node.left, val)
elif val > node.value:
node.right = self.delete(node.right, val)
else:
if not node.left:
return node.right
elif not node.right:
return node.left
temp = self.minValueNode(node.right)
node.value = temp.value
node.right = self.delete(node.right, temp.value)
node.height = 1 + max(self.getHeight(node.left),
self.getHeight(node.right))
balance = self.getBalance(node)
if balance > 1: # LL
if self.getBalance(node.left) >= 0:
return self.rotateRight(node)
else: # LR
node.left = self.rotateLeft(node.left)
return self.rotateRight(node)
if balance < -1: # RR
if self.getBalance(node.right) <= 0:
return self.rotateLeft(node)
else: # RL
node.right = self.rotateRight(node.right)
return self.rotateLeft(node)
return node
def inorder(self, node):
if node:
self.inorder(node.left)
print(node.value, end=' ')
self.inorder(node.right)
tree = AVL()
root = None
for val in [30, 20, 40, 10, 25, 50, 5]:
root = tree.insert(root, val)
print("Inorder after insert:")
tree.inorder(root) # 5 10 20 25 30 40 50
root = tree.delete(root, 40)
print("\nInorder after delete 40:")
tree.inorder(root) # 5 10 20 25 30 50
자바
class Node {
int value, height;
Node left, right;
Node(int val) {
value = val;
height = 1;
}
}
public class AVL {
int getHeight(Node n) {
return (n == null) ? 0 : n.height;
}
int getBalance(Node n) {
return (n == null) ? 0 :
getHeight(n.left) - getHeight(n.right);
}
Node rotateRight(Node y) {
Node x = y.left;
Node T2 = x.right;
x.right = y;
y.left = T2;
y.height = 1 + Math.max(getHeight(y.left),
getHeight(y.right));
x.height = 1 + Math.max(getHeight(x.left),
getHeight(x.right));
return x;
}
Node rotateLeft(Node x) {
Node y = x.right;
Node T2 = y.left;
y.left = x;
x.right = T2;
x.height = 1 + Math.max(getHeight(x.left),
getHeight(x.right));
y.height = 1 + Math.max(getHeight(y.left),
getHeight(y.right));
return y;
}
Node insert(Node node, int val) {
if (node == null)
return new Node(val);
if (val < node.value)
node.left = insert(node.left, val);
else if (val > node.value)
node.right = insert(node.right, val);
else return node;
node.height = 1 + Math.max(getHeight(node.left),
getHeight(node.right));
int balance = getBalance(node);
if (balance > 1 && val < node.left.value)
return rotateRight(node); // LL
if (balance < -1 && val > node.right.value)
return rotateLeft(node); // RR
if (balance > 1 && val > node.left.value) {
node.left = rotateLeft(node.left);
return rotateRight(node); // LR
}
if (balance < -1 && val < node.right.value) {
node.right = rotateRight(node.right);
return rotateLeft(node); // RL
}
return node;
}
Node minValue(Node node) {
while (node.left != null)
node = node.left;
return node;
}
Node delete(Node node, int val) {
if (node == null)
return node;
if (val < node.value)
node.left = delete(node.left, val);
else if (val > node.value)
node.right = delete(node.right, val);
else {
if (node.left == null)
return node.right;
else if (node.right == null)
return node.left;
Node temp = minValue(node.right);
node.value = temp.value;
node.right = delete(node.right,
temp.value);
}
node.height = 1 + Math.max(getHeight(node.left),
getHeight(node.right));
int balance = getBalance(node);
if (balance > 1) {
if (getBalance(node.left) >= 0)
return rotateRight(node); // LL
node.left = rotateLeft(node.left);
return rotateRight(node); // LR
}
if (balance < -1) {
if (getBalance(node.right) <= 0)
return rotateLeft(node); // RR
node.right = rotateRight(node.right);
return rotateLeft(node); // RL
}
return node;
}
void inorder(Node node) {
if (node != null) {
inorder(node.left);
System.out.print(node.value + " ");
inorder(node.right);
}
}
public static void main(String[] args) {
AVL tree = new AVL();
Node root = null;
int[] vals = {30, 20, 40, 10, 25, 50, 5};
for (int v : vals)
root = tree.insert(root, v);
System.out.println("Inorder after insert:");
tree.inorder(root); // 5 10 20 25 30 40 50
root = tree.delete(root, 40);
System.out.println("\nInorder after delete 40:");
tree.inorder(root); // 5 10 20 25 30 50
}
}
4. 레드-블랙 트리
위에서 얘기한 AVL 트리는 엄격한 기준을 적용하기 때문에 삽입, 삭제 시 시간복잡도가 크다는 단점이 있습니다. 이를 보완하기 위해 빠른 탐색속도를 어느정도 유지하면서 삽입, 삭제도 조금 더 빠르게 작업할 수 있는 트리입니다. 즉, 이진탐색 트리와 AVL트리의 중간정도라고 할 수 있습니다.
이 트리에는 5가지 규칙이 있습니다.
첫번째로 모든 노드는 검정 혹은 빨강으로 구분됩니다.
두번째로 루트노드는 검정이어야 합니다.
세번째로 값을 가진 리프의 자식들인 빈 노드들은 모두 검정이어야 합니다.
네번째로 빨강의 자식 노드는 검정이어야 합니다.
마지막은 어떤 노드에서 리프까지 가는 경로는 모두 같은 개수의 검정 노드를 지나야합니다.
레드-블랙 트리는 위 기준에 어긋날때마다 회전 및 색 바꿈을 통해 균형을 유지합니다.
이 트리를 파이썬과 자바코드를 통해서 확인해보겠습니다.
파이썬
RED, BLACK = True, False
class Node:
def __init__(self, val):
self.val = val
self.color = RED # 새 노드는 기본적으로 빨강으로 추가됨
self.left = None
self.right = None
class RBTree:
def __init__(self):
self.root = None
def is_red(self, node):
return bool(node and node.color == RED)
def rotate_left(self, h):
x = h.right
h.right = x.left
x.left = h
x.color = h.color
h.color = RED
return x
def rotate_right(self, h):
x = h.left
h.left = x.right
x.right = h
x.color = h.color
h.color = RED
return x
def flip_colors(self, h):
h.color = RED
h.left.color = BLACK
h.right.color = BLACK
def insert(self, h, val):
if not h:
return Node(val)
if val < h.val:
h.left = self.insert(h.left, val)
elif val > h.val:
h.right = self.insert(h.right, val)
if self.is_red(h.right):
if not self.is_red(h.left):
h = self.rotate_left(h)
if self.is_red(h.left):
if self.is_red(h.left.left):
h = self.rotate_right(h)
if self.is_red(h.left):
if self.is_red(h.right):
self.flip_colors(h)
return h
def move_red_left(self, h):
self.flip_colors(h)
if self.is_red(h.right.left):
h.right = self.rotate_right(h.right)
h = self.rotate_left(h)
self.flip_colors(h)
return h
def move_red_right(self, h):
self.flip_colors(h)
if self.is_red(h.left.left):
h = self.rotate_right(h)
self.flip_colors(h)
return h
def min_node(self, h):
while h.left:
h = h.left
return h
def delete_min(self, h):
if not h.left:
return None
if not self.is_red(h.left):
if not self.is_red(h.left.left):
h = self.move_red_left(h)
h.left = self.delete_min(h.left)
return self.fix_up(h)
def delete(self, h, val):
if val < h.val:
if h.left:
if not self.is_red(h.left):
if not self.is_red(h.left.left):
h = self.move_red_left(h)
h.left = self.delete(h.left, val)
else:
if self.is_red(h.left):
h = self.rotate_right(h)
if val == h.val:
if not h.right:
return None
if h.right:
if not self.is_red(h.right):
if not self.is_red(h.right.left):
h = self.move_red_right(h)
if val == h.val:
mn = self.min_node(h.right)
h.val = mn.val
h.right = self.delete_min(h.right)
else:
h.right = self.delete(h.right, val)
return self.fix_up(h)
def fix_up(self, h):
if self.is_red(h.right):
h = self.rotate_left(h)
if self.is_red(h.left):
if self.is_red(h.left.left):
h = self.rotate_right(h)
if self.is_red(h.left):
if self.is_red(h.right):
self.flip_colors(h)
return h
def inorder(self, h):
if h:
self.inorder(h.left)
print(h.val, end=' ')
self.inorder(h.right)
rbt = RBTree()
for v in [10, 20, 30, 40, 50, 25]:
rbt.root = rbt.insert(rbt.root, v)
rbt.root.color = BLACK
print("Inorder after inserts:")
rbt.inorder(rbt.root) # 10 20 25 30 40 50
rbt.root = rbt.delete(rbt.root, 30)
if rbt.root:
rbt.root.color = BLACK
print("\nInorder after delete 30:")
rbt.inorder(rbt.root) # 10 20 25 40 50
자바
enum Color { RED, BLACK }
class Node {
int val; Color color;
Node left, right;
Node(int v) { val = v; color = Color.RED; } // 새 노드는 기본적으로 빨강으로 추가됨
}
public class RBTree {
private boolean isRed(Node n) {
return n != null && n.color == Color.RED;
}
private Node rotateLeft(Node h) {
Node x = h.right; h.right = x.left;
x.left = h; x.color = h.color;
h.color = Color.RED;
return x;
}
private Node rotateRight(Node h) {
Node x = h.left; h.left = x.right;
x.right = h; x.color = h.color;
h.color = Color.RED;
return x;
}
private void flipColors(Node h) {
h.color = Color.RED;
h.left.color = h.right.color = Color.BLACK;
}
public Node insert(Node h, int v) {
if (h == null) return new Node(v);
if (v < h.val) h.left = insert(h.left, v);
else if (v > h.val) h.right = insert(h.right, v);
// Fix-up
if (isRed(h.right) && !isRed(h.left)) h = rotateLeft(h);
if (isRed(h.left) && isRed(h.left.left)) h = rotateRight(h);
if (isRed(h.left) && isRed(h.right)) flipColors(h);
return h;
}
private Node moveRedLeft(Node h) {
flipColors(h);
if (isRed(h.right.left)) {
h.right = rotateRight(h.right);
h = rotateLeft(h);
flipColors(h);
}
return h;
}
private Node moveRedRight(Node h) {
flipColors(h);
if (isRed(h.left.left)) {
h = rotateRight(h);
flipColors(h);
}
return h;
}
private Node min(Node h) {
while (h.left != null) h = h.left;
return h;
}
public Node deleteMin(Node h) {
if (h.left == null) return null;
if (!isRed(h.left) && !isRed(h.left.left))
h = moveRedLeft(h);
h.left = deleteMin(h.left);
return fixUp(h);
}
private Node fixUp(Node h) {
if (isRed(h.right)) h = rotateLeft(h);
if (isRed(h.left) && isRed(h.left.left)) {
h = rotateRight(h);
}
if (isRed(h.left) && isRed(h.right)) flipColors(h);
return h;
}
public Node delete(Node h, int v) {
if (v < h.val) {
if (h.left != null) {
if (!isRed(h.left) && !isRed(h.left.left))
h = moveRedLeft(h);
h.left = delete(h.left, v);
}
} else {
if (isRed(h.left)) h = rotateRight(h);
if (v == h.val && h.right == null) return null;
if (h.right != null) {
if (!isRed(h.right) && !isRed(h.right.left))
h = moveRedRight(h);
if (v == h.val) {
Node m = min(h.right);
h.val = m.val;
h.right = deleteMin(h.right);
} else
h.right = delete(h.right, v);
}
}
return fixUp(h);
}
public void inorder(Node h) {
if (h != null) {
inorder(h.left);
System.out.print(h.val + " ");
inorder(h.right);
}
}
public static void main(String[] args) {
RBTree t = new RBTree();
Node root = null;
for (int v: new int[]{10,20,30,40,50,25})
root = t.insert(root, v);
root.color = Color.BLACK;
System.out.println("Inorder after inserts:");
t.inorder(root); // 10 20 25 30 40 50
root = t.delete(root, 30);
root.color = Color.BLACK;
System.out.println("\nInorder after delete 30:");
t.inorder(root); // 10 20 25 40 50
}
}
'CS(Computer Science) 이론 > 자료구조' 카테고리의 다른 글
| [자료구조] 해시맵 (0) | 2025.09.17 |
|---|---|
| [자료구조] 힙(heap) (0) | 2025.09.11 |
| [자료구조] 큐(QUEUE) (0) | 2025.09.07 |
| [자료구조] 스택 (0) | 2025.09.06 |
| [자료구조] 연결리스트 (0) | 2025.09.04 |

