탐색이란 여러개의 원소로 구성된 데이터에서 원하는 값을 갖는 원소를 찾는 것을 의미합니다.
이때 주어진 데이터의 형태는 리스트, 트리, 그래프 등이 있고, 탐색 중에서도 내부탐색, 외부탐색이 있습니다.
그리고 탐색을 할때는 초기화, 삽입, 삭제 등 관련 연산등도 고려해야 합니다.
이러한 탐색방법에는 리스트형태(순차 탐색, 이진탐색), 트리형태(이진탐색트리, 2-3-4 트리, 레드-블랙 트리, B-트리), 해시테이블(해시 함수) 등이 있습니다.
1. 순차탐색
리스트 형태로 주어진 원소들을 처음부터 하나씩 차례로(순차) 비교하면서 원하는 값을 갖는 원소를 찾는 방법입니다.
1) 탐색연산의 알고리즘
SequentialSearch(A[],n,x) // A[] : 입력배열, n: 입력크기(탐색할 데이터의 개수), x:탐색 키
{
i=0;
while(i<n && A[i]!=x)
i++;
return i;
}
2) 삽입연산의 알고리즘
SequentialSearch_Insert(A[],n,x) // A[]: 입력배열, n: 입력크기(탐색할 데이터의 개수), x: 삽입할 원소
{
A[n] = x;
return (A,n+1);
}
3) 삭제연산의 알고리즘
SequentialSearch_Delete(A[],n,x) //A[n] :입력배열, n입력크기(탐색할 데이터의 개수), x:삭제할 원소
{
index = SequentialSearch(A,n,x);
if(index == -1) return (A,n);
A[index] = A[n-1];
return (A,n-1);
}
4) 순차탐색의 성능과 특징
탐색을 성공했을 때 1번~n번까지 비교 합니다. 이것을 평균으로 계산해보면 (n+1)/2 번이 됩니다. 반면에 탐색을 실패했을 경우 항상 n번을 비교하게 됩니다. 따라서 탐색의 시간복잡도는 O(n)이 됩니다.
삭제연산의 경우 삭제할 원소의 순차탐색O(n) 후 마지막원소의 이동O(1)이 되므로 삭제연산의 시간복잡도는 O(n)이 됩니다.
삽입연산의 경우 리스트의 마지막에 추가하는데 상수시간만이 필요하므로 시간복잡도는 O(1)이 됩니다.
순차탐색은 모든리스트형태의 입력에 적용가능합니다. 특히 비정렬데이터 탐색에 적합합니다. 또한 탐색과 삭제에 O(n) 시간이 필요하므로 데이터가 큰 경우에는 부적합합니다. 따라서 순차탐색은 정렬되지 않고 크기가 작은 데이터에 적합하다고 할 수 있습니다.
2. 이진탐색
이진탐색은 정렬된 리스트 형태로 주어진 원소들을 절반씩 줄여가면서 원하는 값을 가진 원소를 찾는 방법입니다.
이진탐색은 분할방법이 적용됩니다.
탐색방법은 배열의 가운데 원소 A[mid]와 탐색키를 비교합니다.
만약 탐색키가 A[mid]보다 작다면 원래크기의 절반, 즉 A[mid]보다 왼쪽에 있는 원소들을 대상으로 이진탐색을 순환호출합니다.
반대로 탐색키가 A[mid]보다 크다면 A[mid]보다 오른쪽에 있는 원소들을 대상으로 이진탐색을 호출합니다.
이러한 방법이 반복되기 때문에 탐색을 반복할때마다 대상 원소의 개수가 1/2로 감소합니다. 이것이 가능한 이유는 데이터가 정렬되어 있기 때문입니다.
1) 탐색연산의 알고리즘
BinarySearch(A[],key,Left,Right)
{
if(Left > Right) return (-1)
mid = (Left + Right) / 2;
if(key == A[mid])return mid;
else if(key < A[mid]) BinarySearch(A,key,Left,mid-1)
else BinarySearch(A,key,mid+1,Right);
}
점화식을 확인해보면 T(n) = T(n/2)+ O(1) (n>1),T(1) = 1이기 때문에 T(n) = O(logn)이 됩니다.
2) 초기화 연산의 알고리즘
이진탐색은 리스트가 정렬되어있어야 가능하기 때문에 만약 주어진 배열이 정렬되어 있지 않다면 정렬을 먼저 수행합니다. 이를 초기화 연산이라고 합니다.
BinarySearch_Initialize(A[],n)
{
for(i=0;i<n;i++)
if(A[i] > A[i+1]){
A = Sort(A,n); //오름차순으로 정렬
break;
}
return A;
}
초기화 연산의 성능은 O(nlogn)입니다.
3) 삽입연산의 알고리즘
BinarySearch_Insert(A[],n,x)
{
Left = 0; Right = n-1;
while(Left <= Right){
Mid = (Left + Right) / 2 +Left;
if(x == A[Mid]) return (A,n); // 삽입할 원소가 이미 존재
else if(x < A[Mid]) Right = Mid - 1; // 왼쪽 부분 배열 탐색
else Left = Mid + 1; // 오른쪽 부분배열 탐색
}
for(i=n;i>Left;i--) A[i] = A[i-1]; // A[Left]부터 오른쪽으로 한칸씩 이동 -> 정렬상태를 유지해야 하기 때문에
A[Left] =x; //원소삽입
return (A,n+1);
}
삽입연산의 성능은 O(n)입니다.
4) 삭제연산의 알고리즘
BinarySearch_Delete(A[],n,x)
{
index = BinarySearch(A,x,0,n-1);
if(index == -1) return (A,n); // 삭제할 원소가 존재하지 않음
for(iindexi<n-1;i++) // 삭제할 위치의 오른족 모든 원소를
A[i] = A[i+1]; // 왼쪽으로 한칸씩 이동(원소 삭제) -> 정렬상태를 유지해야하기 때문에
return (A,n-1);
}
삭제연산의 성능은 O(n)이 됩니다.
5) 성능과 특징
이진탐색은 정렬된 리스트에 대해서만 적용이 가능하며, 삽입과 삭제가 빈번한 경우에는 부적합합니다. 왜냐하면 연산 후 리스트의 정렬상태를 유지하기 위해 O(n)의 데이터 이동이 필요하기 때문입니다, 따라서 데이터가 작은 경우에 적합합니다.
3. 이진탐색트리
탐색트리의 조건으로는 한 노드의 왼쪽 서브트리에 있는 모든 키값이 그 노드의 키값보다 작아야하고, 오른쪽 서브트리에 있는 모든 키값은 그 노드의 키값보다 커야합니다.
이진트리이면서 탐색트리라면 이진탐색트리가 됩니다.
1) 탐색연산
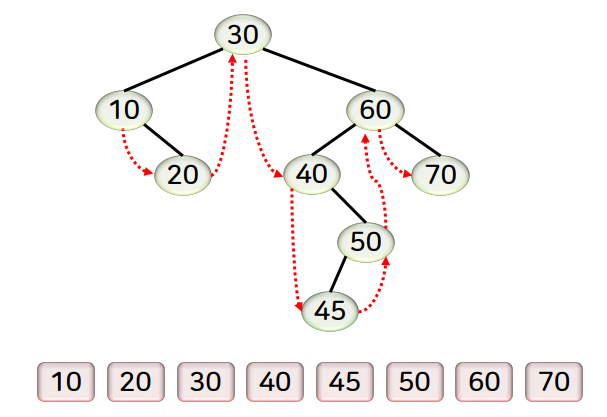
탐색 연산은 루트노드에서부터 시작하여 값의 크기 관계에 따라 트리의 경로를 따라 내려가면서 탐색을 진행합니다.
그림으로 표현하면 아래와 같습니다.

2) 삽입연산
삽입연산은 삽입할 원소를 탐색한 후 탐색이 실패하면 해당 위치에 자식 노드로서 새 노드를 추가합니다.
그림으로 표현하면 아래와 같습니다.


3) 삭제연산
삭제연산은 삭제되는 노드의 자식 노드의 개수에 따라 구분하여 처리합니다.
1] 자식 노드가 없는 경우(리프 노드의 경우) : 남는 노드가 없어 위치 조절을 할 필요가 없습니다.

2] 자식 노드가 1개인 경우 : 자식 노드를 삭제되는 노드의 위치로 올리면서 서브 트리 전체도 따로 올립니다.


3] 자식 노드가 2개인 경우: 삭제되는 노드의 후속자 노드를 삭제되는 노드의 위치로 올리고, 후속자 노드를 삭제되는 노드로 취급하여 자식 노드의 개수에 따라 다시 처리합니다.


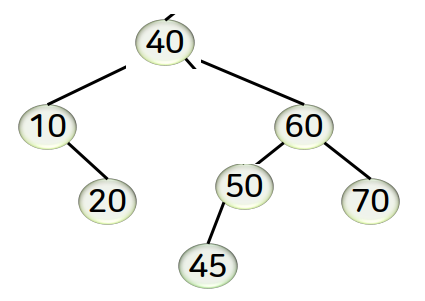
후속자 노드란?
어떤 노드의 바로 다음 키값을 갖는 노드를 의미합니다. 다른말로 계승자 노드라고도 합니다.
아래는 키값의 순서입니다.
4) 성능과 특징
탐색, 삽입, 삭제연산의 시간복잡도는 키값을 비교하는 횟수에 비례합니다. 즉 이진트리의 높이에 따라 달라집니다.
예로 이진트리의 높이가 h라면 O(h)가 됩니다. 또한 이진트리의 형태에 따라 성능이 달라집니다.

이진탐색트리에 삽입연산시 노드의 이동이 없으며, 삭제연산시 상수횟수로 이동합니다. 즉 기존노드의 이동이 거의 발생하지 않습니다.
이진탐색 트리에서 최악의 수행시간을 발생시키는 것은 경사이진트리가 되었을 경우이므로 트리의 균형을 유지하면 O(logn)을 보장할 수 있습니다. 이것을 균형탐색트리라고 합니다. 이 균형 탐색트리에는 2-3-4트리, 레드-블랙트리, B-트리 등이 있습니다.
4. 2-3-4 트리
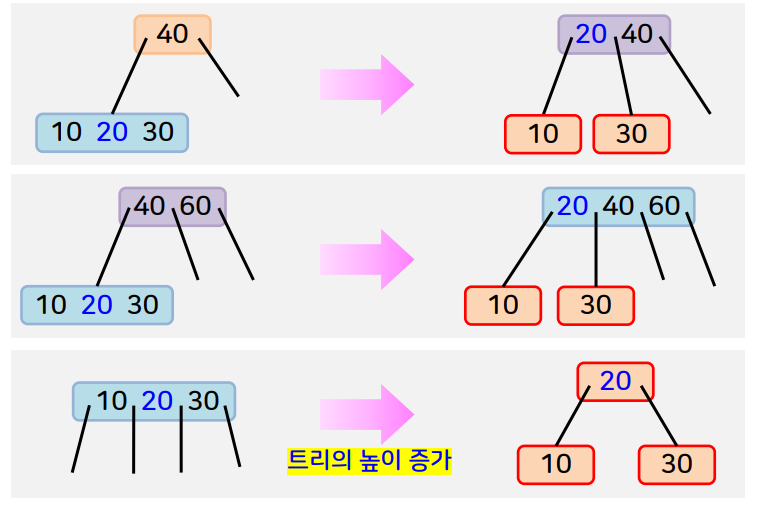
2-3-4 트리는 2-노드,3-노드,4-노드를 만족하는 균형탐색트리입니다.
2-노드란 1개의 키와 2개의 자식을 갖는 노드이며, 3-노드는 2개의 키와 3개의 자식을 갖는 노드입니다. 그리고 4-노드는 3개의 키와 4개의 자식을 갖는 노드입니다. 2-3-4 트리의 형태는 아래와 같습니다.

1) 탐색연산
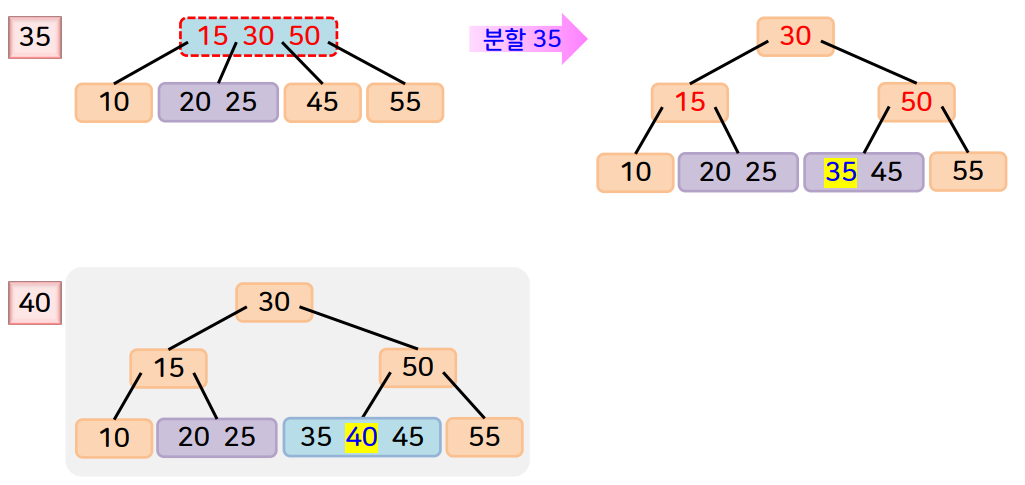
탐색연산은 기본적으로 이진탐색트리와 유사합니다. 만약 40을 찾고 싶다면 루트노드에서 첫번째 키와 비교합니다.
첫번째 키보다 크다면 두번째 키와 비교합니다. 두번째 키보다 작다면 자식노드로 내려갑니다. 이것을 반복하여 탐색합니다.

2) 삽입연산
탐색과정에서 4-노드를 만나면 항상 노드 분할을 우선 수행합니다.
노드 분할은 아래순서로 진행합니다.


노드 분할의 유형은 2-노드,3-노드,4-노드인 유형으로 나뉩니다.
경우에 따라 삽입은 아래와 같이 됩니다.
삽입연산의 예제는 아래와 같습니다.


3) 성능과 특징
균형탐색트리이기 때문에 성능은 O(logn)이 됩니다.
루트 노드가 분할되는 경우에 한해서 모든 노드의 레벨이 동일하게 1씩 증가하기 때문에 삽입 및 삭제가 일어나도 경사트리가 되지 않습니다.
단점으로는 2-3-4 트리를 그대로 구현하면 노드의 구조가 복잡해서 이진탐색트리보다 더 느려질 가능성이 많습니다.
5. 레드 - 블랙 트리
레드 - 블랙 트리는 기본적으로 이진탐색 트리이며, 균형 탐색 트리입니다. 이러한 레드 - 블랙 트리는 아래 성질을 모두 만족해야 합니다.
성질 1 : 모든 노드는 검정이거나 빨강입니다.
성질 2 : 루트 노드와 리프노드는 검정입니다. → 모든 리프노드는 Null 노드입니다.
성질 3 : 빨강 노드의 부모 노드는 항상 검정이다. → 빨강 노드가 연달아 나타날 수 없습니다.
성질 4 : 임의의 노드로부터 리프 노드까지의 경로상에는 동일한 개수의 검정노드가 존재합니다.
성질 5 : 한 노드의 왼쪽 서브트리에 있는 모든 키값이 그 노드의 키값보다 작아야합니다.
성질 6 : 한 노드의 오른쪽 서브트리에 있는 모든 키값은 그 노드의 키값보다 커야합니다.
-> 성질5, 6은 이진탐색의 성질입니다.
레드 - 블랙 트리는 아래와 같은 형태를 지닙니다.

1) 탐색 연산
이진탐색 트리의 탐색 방법과 동일합니다.

2) 삽입연산


두번째 케이스를 살펴보겠습니다


따라서 삽입연산을 할때는 빨강 노드가 연달아 나타날경우에 적용하는 규칙이 필요합니다.
규칙1 : 부모 노드의 형제노드가 빨강인경우
→ 부모노드, 부모노드의 형제노드, 부모노드의 부모노드의 색깔을 모두 변경합니다.
규칙2 : 부모노드의 형제노드가 검정이고, 현재 노드의 키값이 부모노드와 부모노드의 부모노드의 키값의 사이인 경우
→ 현재 노드와 부모노드를 회전시킵니다.
규칙3 : 부모 노드의 형제 노드가 검정이고, 현재 노드의 키 값보다 부모노드와 부모노드의 부모노드의 키 값이 크거나 작을 경우
→ 부모 노드와 부모노드의 부모노드를 회전시키고 색깔을 변경합니다.



우회전하기 때문에 40이 60자리로 이동하고 60이 한칸 내려옵니다. 그리고 40에 붙어있던 자식 노드 중 하나를 포기하여 60에 붙입니다.


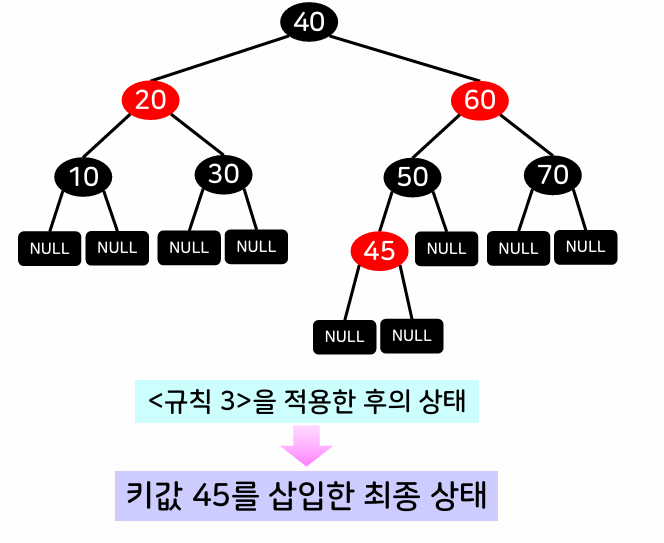
3) 성능과 특징
레드 - 블랙 트리는 어떤 두 리프노드의 레벨 차이가 2배를 넘지 않는 균형탐색 트리입니다.
성질3에 의해 빨강 노드가 연달아 나타날 수 없고, 성질4에 의해 루트노드의 리프노드의 경로상에 동일한 개수의 검정 노드가 존재하기 때문에 루트노드에서 리프노드의 경로상에는 빨강노드의 개수보다 항상 검정노드의 개수가 많습니다.
2-3-4 트리의 단점을 이진탐색트리로 표현한 것입니다. 따라서 레드 - 블랙 트리에서는 최악의 경우 트리의 높이가 O(logn)입니다. 따라서 성능도 O(logn)이 됩니다.
6. B- 트리
B - 트리는 균형탐색트리이며 아래 성질을 모두 만족해야 합니다.
성질1 : 루트 노드는 1개 이상 2t개 미만의 오름차순으로 정렬된 키를 가집니다. (t는 자연수)
성질2 : 루트 노드가 아닌 모든 노드는 (t-1) 개 이상 2t개 미만의 오름차순으로 정렬된 키를 가집니다.
성질3 : 내부 노드는 자신이 가진 키의 개수보다 하나 더 많은 자식 노드를 가집니다.
성질4 : 각 노드의 한 키의 왼쪽 서브트리에 있는 모든 키 값은 그 키값보다 작아야 합니다.
성질5 : 각 노드의 한 키의 오른쪽 서브트리에 있는 모든 키 값은 그 키값보다 커야합니다.
성질6 : 모든 리프 노드의 레벨은 동일합니다.
아래 사진과 같은 형태를 가집니다.

1) 탐색연산

탐색키가 루트노드인 10보다 크기때문에 오른쪽으로 내려갑니다. 그리고 자식노드에서 하나씩 비교하면서 13하고 19사이에 있기 때문에 13~19사이에 있는 자식 노드로 내려갑니다. 오름차순으로 정렬되어있기 때문에 이렇게 찾을 수 있습니다.
2) 삽입연산

예제)

t(노드의 높이)가 3이므로 13,19,22,26,29 중 13과 19로 분할하고 26,29로 분할하고 3번째인 22는 부모노드로 이동합니다.

t가 3이므로 가장 아래의 노드의 키의 개수는 3-1 = 2 <= key <= 2*3-1 = 5이 되어 총 5개까지의 원소를 가질 수 있습니다. 따라서 위 그림의 위치에 삽입할 18이 들어가게 됩니다.
3) 성능과 특징
시간복잡도는 O(logn)이 됩니다.
B- 트리의 특징으로는 내부탐색과 외부탐색에 모두 활용할 수 있습니다.
내부탐색의 경우 t=2 또는 t=3정도의 작은 값으로 지정합니다. 이때 t=2일 경우 2-3-4트리가 됩니다.
외부 탐색의 경우 디스크를 사용하는 경우라면 t를 충분히 크게 지정합니다. 이 때 한 노드의 크기가 디스크의 한 블록에 저장되도록 합니다.
7. 해시테이블
해싱이란 키값을 기반으로 데이터의 저장위치를 직접 계산함으로써 상수시간 내에 데이터를 저장, 삭제, 탐색할 수 있는 방법입니다.


1) 해시함수

1] 제산잔여법

위 그림에서 16은 2의 4제곱이기 때문에 아래 4개의 비트만 확인합니다. 이때 39,3751은 둘다 7이 나오므로 주소가 동일하게 7이 됩니다.
2] 비닝

3] 중간제곱법

4] 문자열을 위한 비닝

5] 문자열을 위한 단순합

6] 문자열을 위한 가중합

2) 충돌 해결방법
충돌이란 서로 다른 키값 x,y에 대하여 h(x) = h(y)인 경우를 의미합니다.
1] 개방해싱
연쇄법이라고도 하며 충돌된 데이터를 테이블 밖의 별도의 장소에 저장 및 관리하는 방법입니다. 연결 리스트 사용합니다.

2] 폐쇄 해싱_ 버킷해싱

3] 폐쇄해싱_선형탐사


9530까지는 크게 문제가 발생하지 않지만 2007을 해싱할때 계속해서 충돌이 발생하게됩니다.
4] 폐쇄해싱_이차탐사



5] 폐쇄해싱_이중해싱

3) 삭제연산
삭제연산을 할때에는 두가지를 고려해야합니다.
첫번째로 데이터의 삭제가 차후의 탐색을 방해하지 말아야합니다. 삭제한 데이터를 빈 슬롯으로 두면 탐색이 해당 슬롯에서 종료되므로 그 이후의 데이터는 고립됩니다.
두번재로 삭제로 생긴 빈 슬롯은 나중에 삽입과정에서 사용되어야 합니다.
이를 위해서 비석이라는 개념이 사용됩니다.
비석이란 삭제된 데이터의 위치에 특별한 표시를 하는 방법입니다. 이 비석을 사용하면 탐색 시 탐색하는 동안 비석을 만나게 되면 탐색을 계속 진행하며, 삽입시 비석이 표시된 위치를 빈 위치로 간주하여 새 데이터를 삽입할 수 있습니다.
다만 비석의 개수가 증가할 수록 평균 탐색거리가 증가한다는 문제가 발생할 수 있습니다.
'CS(Computer Science) 이론 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 그래프 알고리즘 (0) | 2024.05.20 |
|---|---|
| [알고리즘] 그래프의 기본 개념과 순회 (0) | 2024.05.13 |
| [알고리즘] 데이터 분포 기반 알고리즘 (1) | 2024.04.27 |
| [알고리즘] 비교 기반 알고리즘 (0) | 2024.04.27 |
| [알고리즘] 정렬 관련 개념 (0) | 2024.04.27 |

