1. 그래프란?
그래프란 정점 또는 노(vertex)와 간선(edge)로 구성된 비선형 자료구조로 다양한 현실세계의 문제를 모델링하는데 사용됩니다.

위의 간선(edge)에는 방향성과 가중치가 있을 수도 있고 없을 수도 있습니다.
2. 그래프에서 사용되는 주요 용어
1) 인접, 부수
두 정점 x,y 사이에 간선이 있으면 정점 x와 y는 인접한다고 하며, 해당간선은 정점 x와 y에 부수되었다고 합니다.
2) 부분 그래프
원래의 그래프에서 일부의 정점이나 간선을 제외하여 만든 그래프를 부분 그래프라고 합니다. 위 그림에서 G2는 G1의 부분 그래프라고 할 수 있습니다.
3) 경로
그래프에서 정점 v1으로부터 vn까지의 경로란 간선 (v1,v2), (v2,v3),....,(v(n-1),vn) 으로 연결된 v1,v2,...,vn을 의미하며
이 때 경로상의 존재하는 간선의 개수를 경로의 길이라고 합니다.
4)차수
해당 정점에 부수된 간선의 수를 의미하며, 방향 그래프에서는 이러한 차수를 세분화하여 정점으로 들어오는 간선의 수를 진입차수라고 하고 그 정점에서 나가는 간선의 수를 진출차수라고 합니다.
5)단순경로
한 경로상에서 처음과 마지막 정점을 제외한 모든 정점이 서로 다른 경로를 의미합니다.
6) 사이클
처음과 마지막 정점이 같은 단순경로를 의미하며 특히 사이클이면서 경로의 길이가 1인 경로를 루프라고합니다.
7) 연결
무방향 그래프에서 서로 다른 정점 u,v의 모든 쌍에 대해서 u에서 v까지 경로가 있으면 그래프는 연결되었다고합니다. 방향 그래프의 경우에는 서로 다른 두 정점 u,v의 모든 쌍에 대해서 u에서 v로의 방향 경로와 v에서 u로의 방향경로가 존재하면 그 방향 그래프는 강력하게 연결되었다고 하고 그렇지 않으면 약하게 연결되었다고 합니다.
3. 그래프의 구현방법
그래프의 간선은 리스트 또는 행렬방식으로 나타낼 수 있습니다.

입력방식은 아래와 같습니다.
1) 방향성과 가중치가 없는 그래프

위 그래프는 방향성이 없으므로 정점과 정점사이의 화살표가 없이 선으로 이어져있는 것을 볼 수 있습니다.
그리고 옆의 리스트를 보면 정점에 연결된 선이 리스트로 생성된 것을 확인할 수 있습니다.
예를 들면 정점 0에는 정점 2,3과 연결되어 있으므로 리스트의 0번에는 2,3이 있고, 2번에는 연결된 0,4 그리고 3번에는 마찬가지로 연결된 0이 있는 것을 확인할 수 있습니다. 무방향성은 즉 양방향이기 때문에 행렬로 확인해보면 (0,2)도 1이며 (2,0)도 1임을 확인할 수 있습니다.
2) 방향성이 있는 그래프
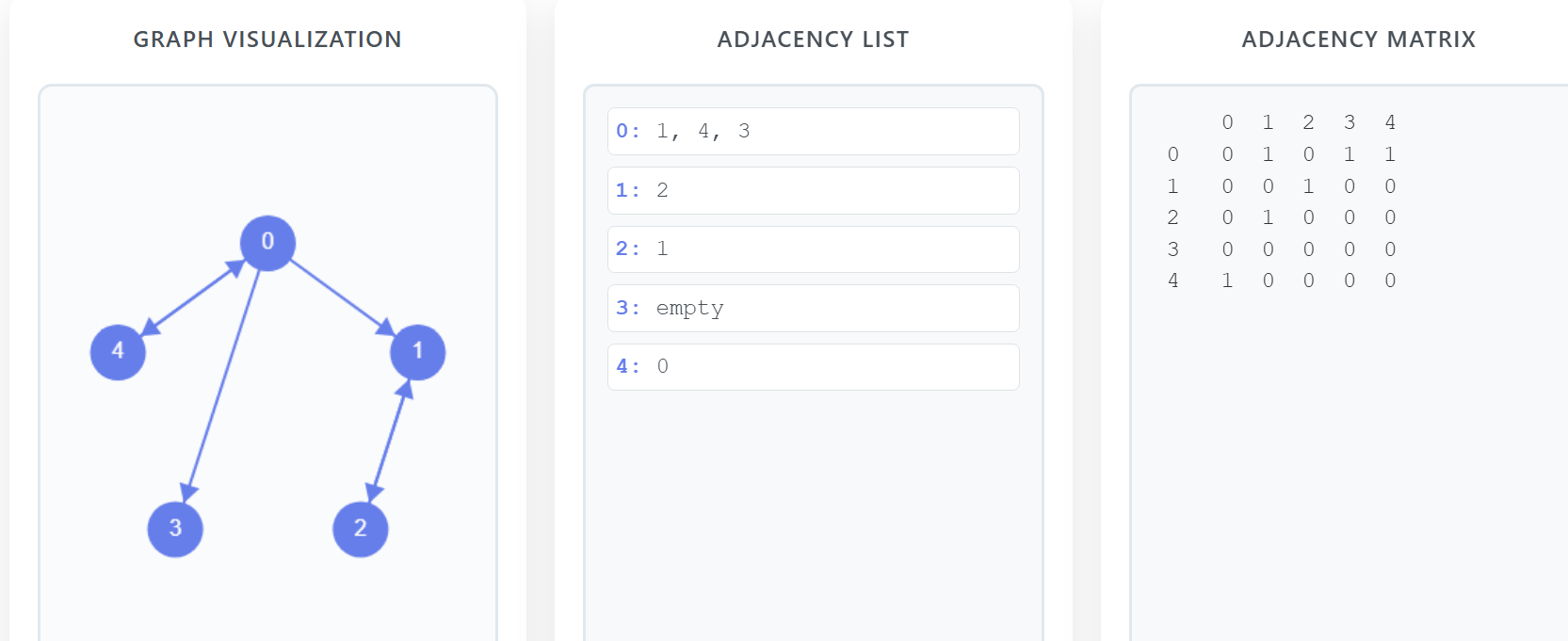
위 그림을 보면 이번에는 화살표가 있는 것을 볼 수 있습니다. 즉, 방향성이 있다는 것은 단방향도 될수 있고 양방향도 될 수 있다는 의미입니다. 리스트에 보면 0번 인덱스는 1,3,4가 있지만 단방향 화살표만 있는 3번에는 0번이 없는 것을 확인할 수 있습니다.
행렬도 마찬가지로 (0,3)은 1이지만 (3,0)은 0인것을 확인할 수 있습니다.
3) 가중치가 있는 그래프

가중치가 있는 그래프는 위 그림처럼 간선에 숫자가 나타납니다. 그리고 리스트에는 괄호안에 가중치가 적히며, 행렬일때는 행과 열의 값에 가중치가 있는 것을 확인할 수 있습니다.
그래프를 파이썬과 자바의 코드로 확인해보겠습니다
1] 인접리스트 방식
파이썬
class Graph:
def __init__(self, directed=False):
self.directed = directed
self.adj_list = {}
def add_edge(self, src, dest, weight=1): ## dest는 향할 노드(정점), weight= 가중치
if src not in self.adj_list:
self.adj_list[src] = []
self.adj_list[src].append((dest, weight))
if not self.directed:
if dest not in self.adj_list:
self.adj_list[dest] = []
self.adj_list[dest].append((src, weight))
def print_graph(self):
for node in self.adj_list:
print(f"{node} -> {self.adj_list[node]}")
print("Undirected, unweighted:")
g1 = Graph(directed=False) ## 방향성이 없는 그래프
g1.add_edge(0, 1)
g1.add_edge(0, 2)
g1.print_graph()
# 0 -> [(1, 1), (2, 1)]
# 1 -> [(0, 1)]
# 2 -> [(0, 1)]
print("\nDirected, weighted:")
g2 = Graph(directed=True) ## 방향성이 있는 그래프
g2.add_edge(0, 1, 4)
g2.add_edge(1, 2, 5)
g2.print_graph()
# 0 -> [(1, 4)]
# 1 -> [(2, 5)]
자바
import java.util.*;
class Edge {
int dest, weight; // dest = 향할 노드(정점)의 번호, weight= 가중치
Edge(int dest, int weight) {
this.dest = dest;
this.weight = weight;
}
}
public class Graph {
private boolean directed;
private Map<Integer, List<Edge>> adjList;
public Graph(boolean directed) {
this.directed = directed;
adjList = new HashMap<>();
}
public void addEdge(int src, int dest, int weight) {
adjList.putIfAbsent(src, new ArrayList<>());
adjList.get(src).add(new Edge(dest, weight));
if (!directed) {
adjList.putIfAbsent(dest, new ArrayList<>());
adjList.get(dest).add(new Edge(src, weight));
}
}
public void printGraph() {
for (int node : adjList.keySet()) {
System.out.print(node + " -> ");
for (Edge edge : adjList.get(node)) {
System.out.print("(" + edge.dest + ", " + edge.weight + ") ");
}
System.out.println();
}
}
public static void main(String[] args) {
System.out.println("Undirected, unweighted:");
Graph g1 = new Graph(false);
g1.addEdge(0, 1, 1);
g1.addEdge(0, 2, 1);
g1.printGraph();
// 0 -> (1, 1) (2, 1)
// 1 -> (0, 1)
// 2 -> (0, 1)
System.out.println("\nDirected, weighted:");
Graph g2 = new Graph(true);
g2.addEdge(0, 1, 4);
g2.addEdge(1, 2, 5);
g2.printGraph();
// 0 -> (1, 4)
// 1 -> (2, 5)
}
}
2] 인접행렬 방식
파이썬
class Graph:
def __init__(self, num_vertices, directed=False):
self.directed = directed
self.V = num_vertices
self.matrix = [
[0] * self.V for _ in range(self.V)
]
def add_edge(self, src, dest, weight=1):
self.matrix[src][dest] = weight
if not self.directed:
self.matrix[dest][src] = weight
def print_graph(self):
for row in self.matrix:
print(row)
print("Undirected, unweighted:")
g1 = Graph(3, directed=False) # 인스턴스 생성시 노드(정점)수를 미리 넣어줌
g1.add_edge(0, 1)
g1.add_edge(0, 2)
g1.print_graph()
# [0, 1, 1]
# [1, 0, 0]
# [1, 0, 0]
print("\nDirected, weighted:")
g2 = Graph(3, directed=True)
g2.add_edge(0, 1, 4)
g2.add_edge(1, 2, 5)
g2.print_graph()
# [0, 4, 0]
# [0, 0, 5]
# [0, 0, 0]
자바
public class Graph {
private boolean directed;
private int[][] matrix;
private int V;
public Graph(int numVertices, boolean directed) {
this.directed = directed;
this.V = numVertices;
matrix = new int[V][V];
}
public void addEdge(int src, int dest, int weight) {
matrix[src][dest] = weight;
if (!directed) {
matrix[dest][src] = weight;
}
}
public void printGraph() {
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
}
public static void main(String[] args) {
System.out.println("Undirected, unweighted:");
Graph g1 = new Graph(3, false);
g1.addEdge(0, 1, 1);
g1.addEdge(0, 2, 1);
g1.printGraph();
// 0 1 1
// 1 0 0
// 1 0 0
System.out.println("\nDirected, weighted:");
Graph g2 = new Graph(3, true);
g2.addEdge(0, 1, 4);
g2.addEdge(1, 2, 5);
g2.printGraph();
// 0 4 0
// 0 0 5
// 0 0 0
}
}4. 그래프 순회
그래프 순회란 그래프의 모든 정점을 체계적으로 한번씩 방문하는 것을 의미합니다.
1) 탐색 과정에서의 정점의 구분

2) 깊이 우선 탐색(DFS)
깊이 우선 탐색은 한 정점을 시작으로 인접한 정점 중 한곳으로 끝까지 이동한 후 더 이상 갈 수 없 수 없을때 다시 돌아가 다른 경로를 탐색하는 방법입니다.
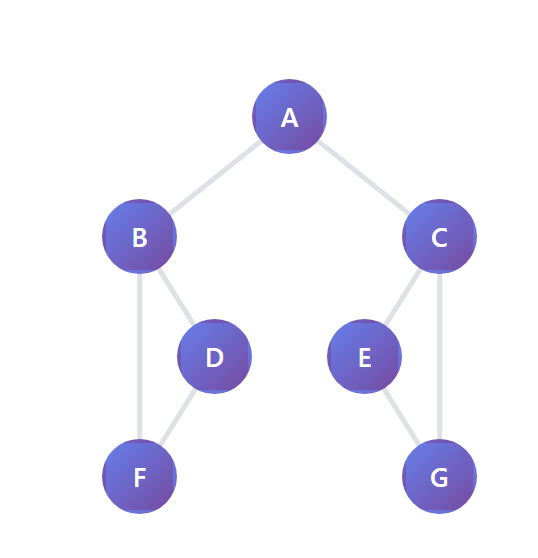
위와 같은 그래프에서 A에서 시작한다면 A->B->D->F 까지 간 후 C로 이동하는 것입니다.
깊이 우선 탐색의 시간복잡도는 O(V+E) 즉, 정점과 간선의 개수의 합만큼의 시간이 걸립니다.
깊이 우선 탐색은 스택구조를 사용해서 구현합니다.
현재 정점에 인접한 정점이 없어서 더 이상 탐색을 진행할 수 없다면 거꾸로 되돌아가면서 아직 탐색하지 않은 인접한 정점을 찾아서 탐색을 진행합니다.
깊이 우선탐색의 처리과정은 아래와 같은 순서대로 진행합니다.
첫번째 시작정점을 스택에 삽입합니다.
두번째 스택의 top에 있는 정점에 대한 주변 정점이 존재하면 그 중 하나의 정점을 스택에 삽입하고 방문한 정점으로 처리합니다. 만약에 주변 정점이 없다면 스택의 top에 있는 정점을 제거합니다.
세번째 스택에 더 이상의 정점이 없을때까지 두번째과정을 반복합니다.
깊이 우선탐색의 알고리즘은 아래와 같습니다.
DepthFirstSearch(G,s){ // G: 입력 그래프, s: 시작정점
Push(Stack,s);
while(Stack != null){
c = Stack의 top에 있는 정점;
c.visted = true;
정점C를 방문 정점으로 출력;
do{
for(v <- c의 모든 인접한 정점){
if(v.visited == false)
Push(Stack,v)후 while문으로 이동;
}
c = Pop(Stack);
}while(Stack != null);
}
}
파이썬
class Graph:
def __init__(self, vertices):
self.V = vertices
self.adj = {i: [] for i in range(vertices)} ## 무방향 무가중치 그래프
def add_edge(self, u, v): ## 연결할 정점 u, v
self.adj[u].append(v)
self.adj[v].append(u)
def dfs(self, start):
visited = set()
def visit(v):
visited.add(v)
print(v, end=' ')
for neighbor in self.adj[v]:
if neighbor not in visited:
visit(neighbor)
visit(start)
print()
g = Graph(5)
g.add_edge(0, 1)
g.add_edge(0, 2)
g.add_edge(1, 3)
g.add_edge(1, 4)
print("DFS:")
g.dfs(0) # 0 1 3 4 2
자바
import java.util.*;
public class Graph {
private int V;
private List<List<Integer>> adj;
public Graph(int vertices) {
V = vertices;
adj = new ArrayList<>();
for (int i = 0; i < V; i++)
adj.add(new ArrayList<>());
}
public void addEdge(int u, int v) {
adj.get(u).add(v);
adj.get(v).add(u);
}
public void dfs(int start) {
boolean[] visited = new boolean[V];
dfsVisit(start, visited);
System.out.println();
}
private void dfsVisit(int v, boolean[] visited) {
visited[v] = true;
System.out.print(v + " ");
for (int neighbor : adj.get(v)) {
if (!visited[neighbor])
dfsVisit(neighbor, visited);
}
}
public static void main(String[] args) {
Graph g = new Graph(5);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 3);
g.addEdge(1, 4);
System.out.println("DFS:");
g.dfs(0); // 0 1 3 4 2
}
}
그림으로 예를 들면 아래와 같습니다.




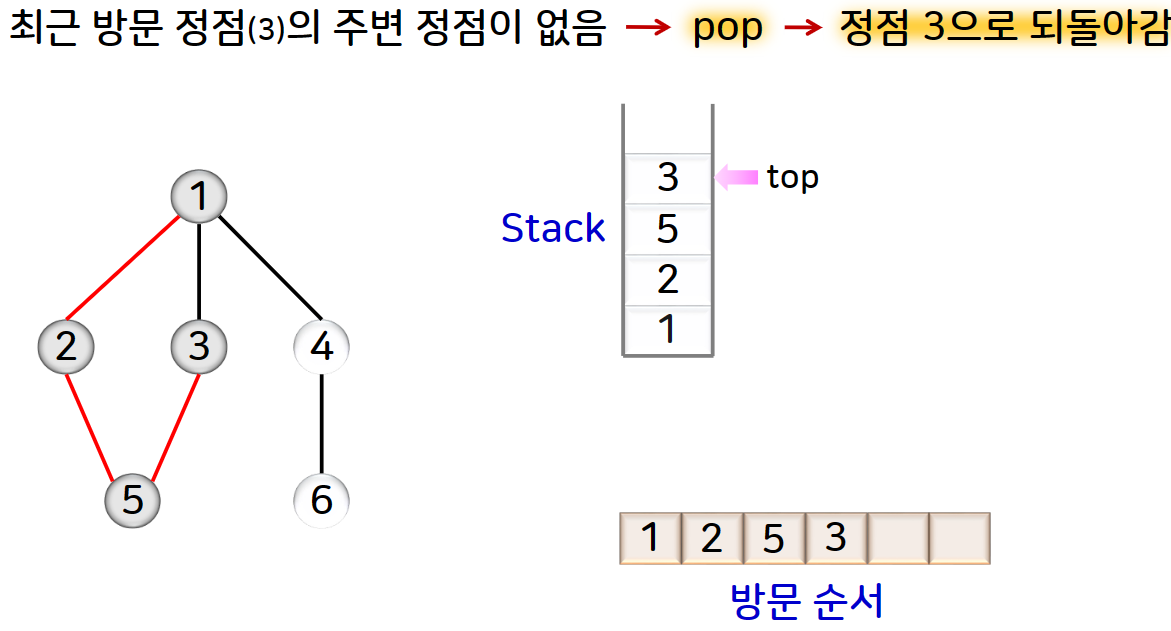
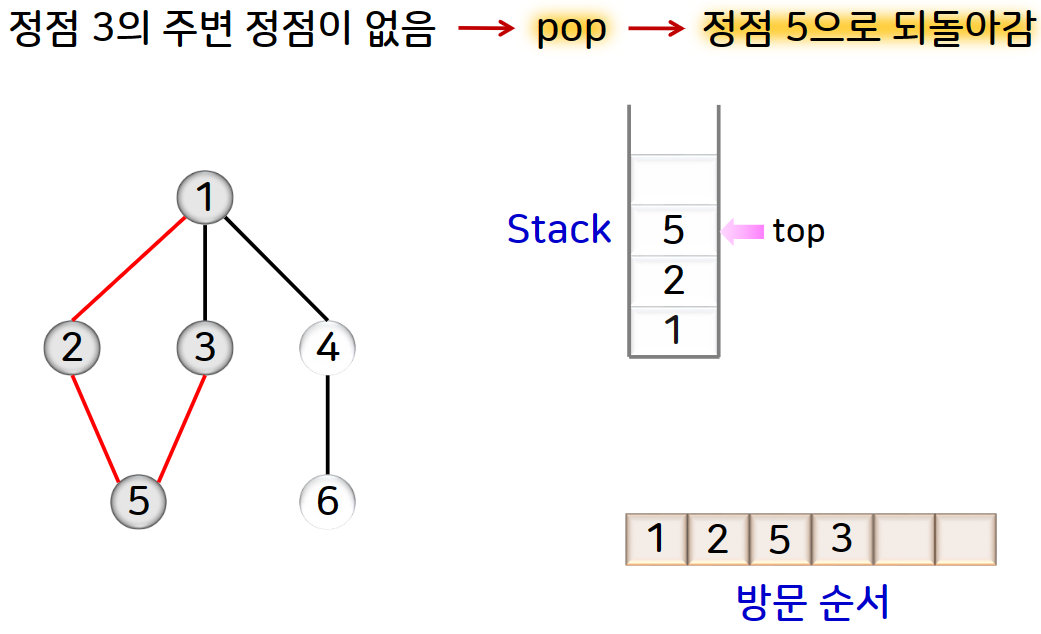


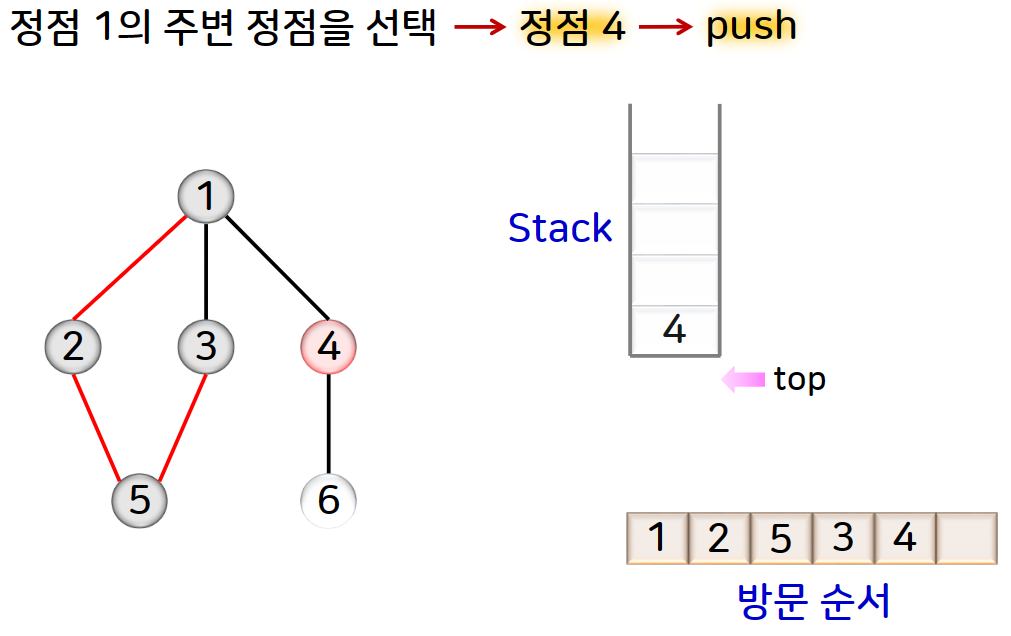


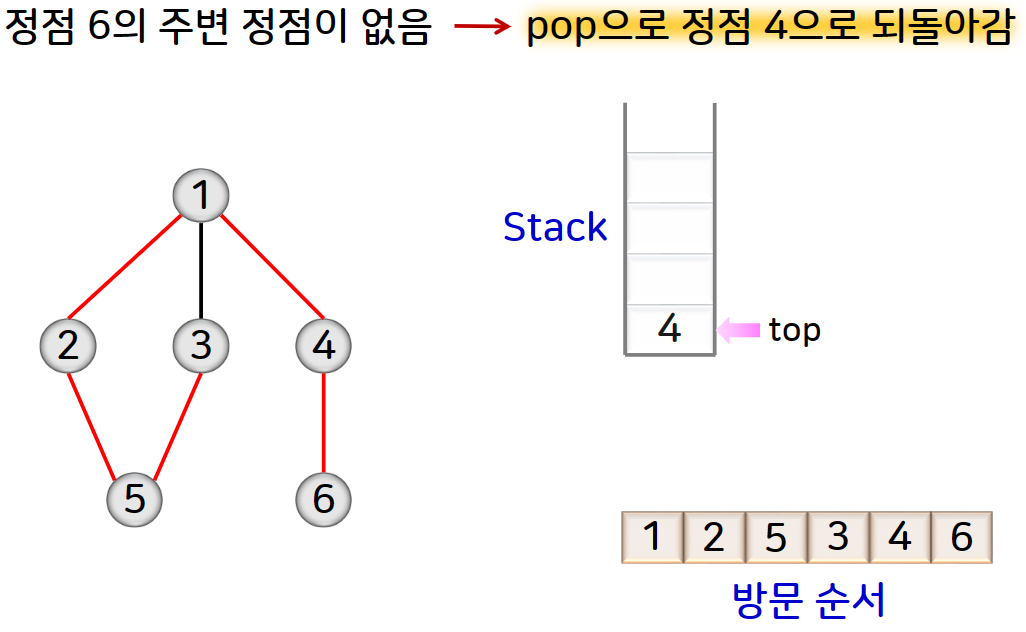

DFS를 수행하는 과정에서 방문한 정점과 그때 사용된 간선으로 구성되는 트리를 깊이 우선 트리라고 합니다.
두번째 그림예제는 아래와 같습니다.

방문순서는 총 10가지가 나옵니다.
깊이 우선 탐색의 성능은 인접 리스트일 경우 O(정점의 개수+ 간선의 개수) 가 되며
인접행렬로 표현했을때는 O(정점의 개수의 제곱)으로 표현됩니다.
그리고 싶이 우선탐색은 아래 코드처럼 순환 알고리즘으로도 표현할 수 있습니다.
DFS_recursion(G,current){
current.visited = true;
방문정점으로 current 출력;
for(next <- current의 모든 인접한 정점){
if(next.visited == false)
DFS_recursion(G,next);
}
}
3) 너비 우선 탐색
시작 정점을 기준으로 거리가 가장 가깝게 인접한 정점을 우선으로 모두 방문한 후 시작 정점과의 거리가 점점 멀어지는 순서로 인접 정점들을 탐색하는 방법입니다.이때 거리란 시작 정점으로부터의 경로의 길이입니다.

위 그래프를 예로들면 A -> B -> C -> D ... 순으로 이동한다고 볼 수 있습니다.
너비 우선 탐색에서는 큐를 사용하여 주변 정점을 관리합니다.
너비 우선 탐색의 알고리즘은 아래와 같습니다.
BreadthFirstSearch(G,s){
Enqueue(Queue,s);
s.flag = true;
while(Queue != null){
c = Dequeue(Queue);
정점 c를 방문 정점으로 출력;
for(v <- c의 모든 인접한 정점)
if(v.flag == false){
Enqueue(Queue,v);
v.flag = true;
}
}
}
파이썬
from collections import deque
class Graph:
def __init__(self, vertices):
self.V = vertices
self.adj = {i: [] for i in range(vertices)}
def add_edge(self, u, v):
self.adj[u].append(v)
self.adj[v].append(u)
def bfs(self, start):
visited = set()
queue = deque([start])
visited.add(start)
while queue:
v = queue.popleft()
print(v, end=' ')
for neighbor in self.adj[v]:
if neighbor not in visited:
visited.add(neighbor)
queue.append(neighbor)
print()
g = Graph(5)
g.add_edge(0, 1)
g.add_edge(0, 2)
g.add_edge(1, 3)
g.add_edge(1, 4)
print("BFS:")
g.bfs(0) # 0 1 2 3 4
자바
import java.util.*;
public class Graph {
private int V;
private List<List<Integer>> adj;
public Graph(int vertices) {
V = vertices;
adj = new ArrayList<>();
for (int i = 0; i < V; i++)
adj.add(new ArrayList<>());
}
public void addEdge(int u, int v) {
adj.get(u).add(v);
adj.get(v).add(u);
}
public void bfs(int start) {
boolean[] visited = new boolean[V];
Queue<Integer> queue = new LinkedList<>();
queue.add(start);
visited[start] = true;
while (!queue.isEmpty()) {
int v = queue.poll();
System.out.print(v + " ");
for (int neighbor : adj.get(v)) {
if (!visited[neighbor]) {
visited[neighbor] = true;
queue.add(neighbor);
}
}
}
System.out.println();
}
public static void main(String[] args) {
Graph g = new Graph(5);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 3);
g.addEdge(1, 4);
System.out.println("DFS:");
g.dfs(0); // 0 1 3 4 2
System.out.println("BFS:");
g.bfs(0); // 0 1 2 3 4
}
}
너비 우선 탐색의 예를 그림으로 확인해보겠습니다.

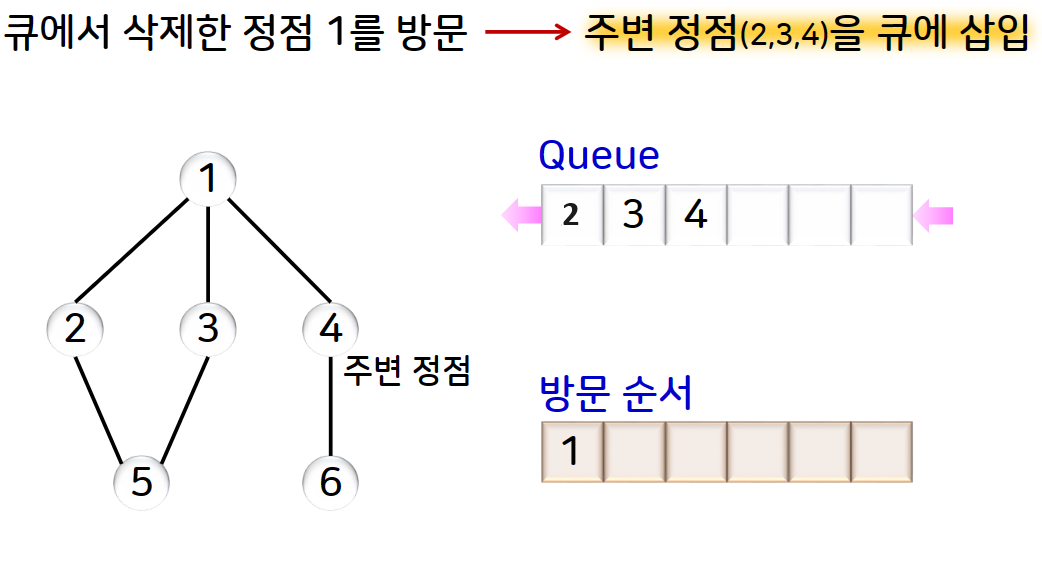

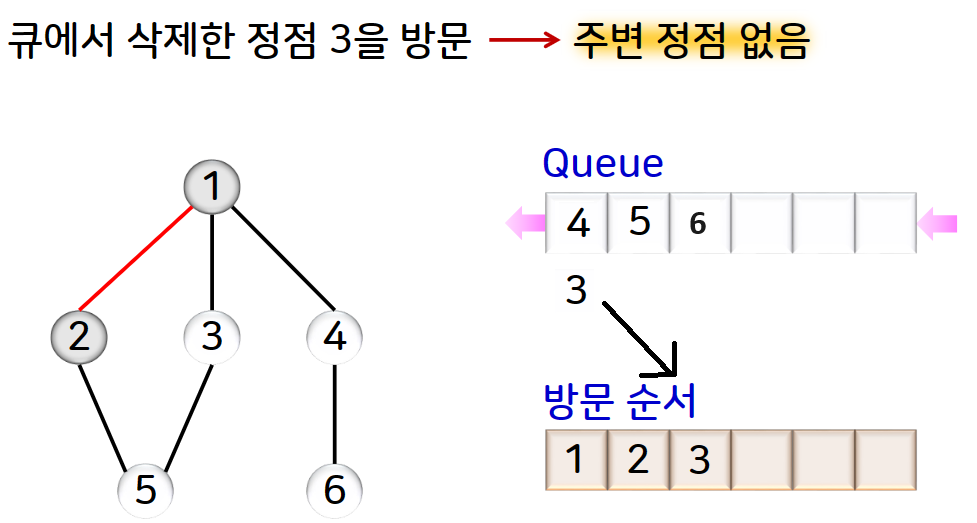

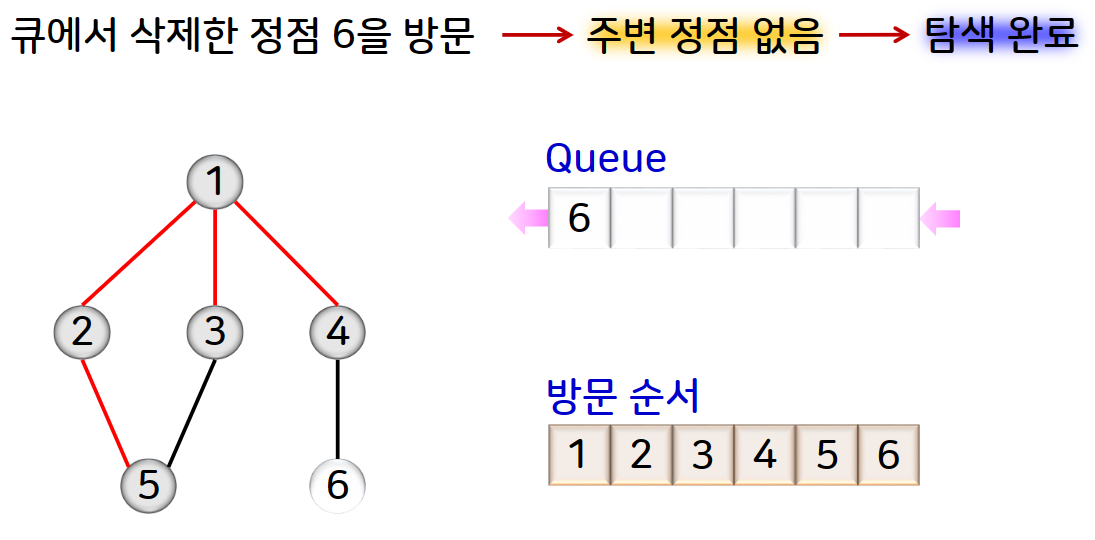
두번째 그림예제는 아래와 같습니다.

1의 주변 정점 2,4,6,7을 일렬로 나열하는 것과 같기 때문에 4!이 되어 24가지가 나타납니다.
4) 그래프 순회의 응용
1] 위상정렬
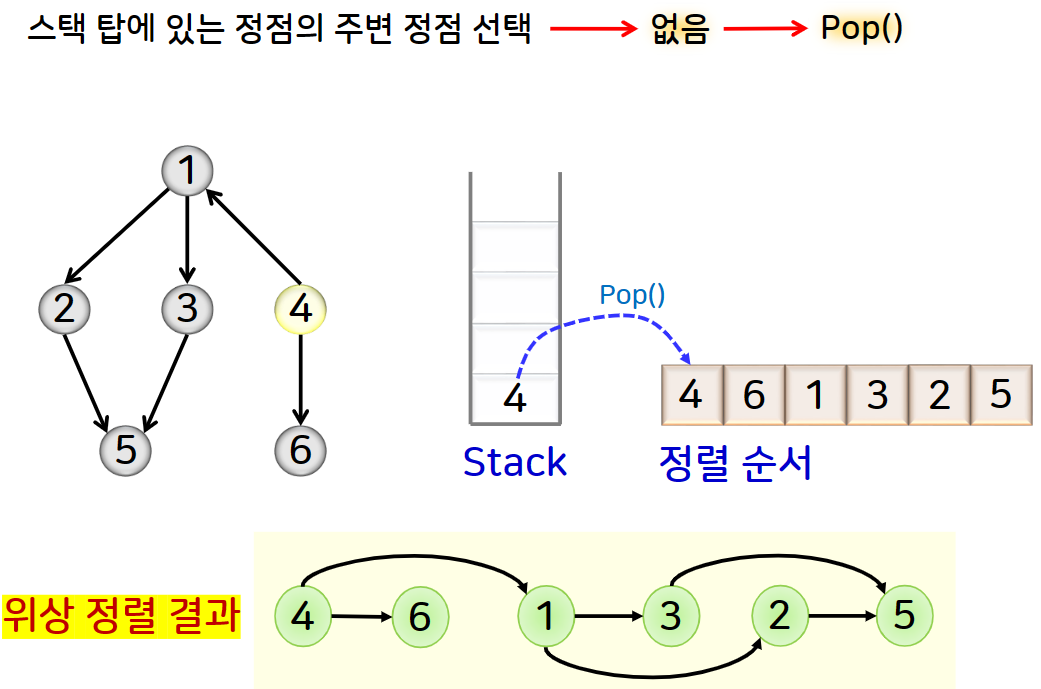
무사이클 방향 그래프에서 모든 간선이 한방향으로 향하도록 정점을 한줄로 나열하는 것을 위상정렬이라고 합니다.

이러한 위상정렬은 깊이 우선탐색을 활용하여 구합니다.
즉 DFS를 수행하다가 더 이상 주변정점이 없어서 되돌아갈 때, 스택에서 삭제되는 정점을 역순으로 나열하면 됩니다.
예제를 그림으로 확인해보겠습니다.

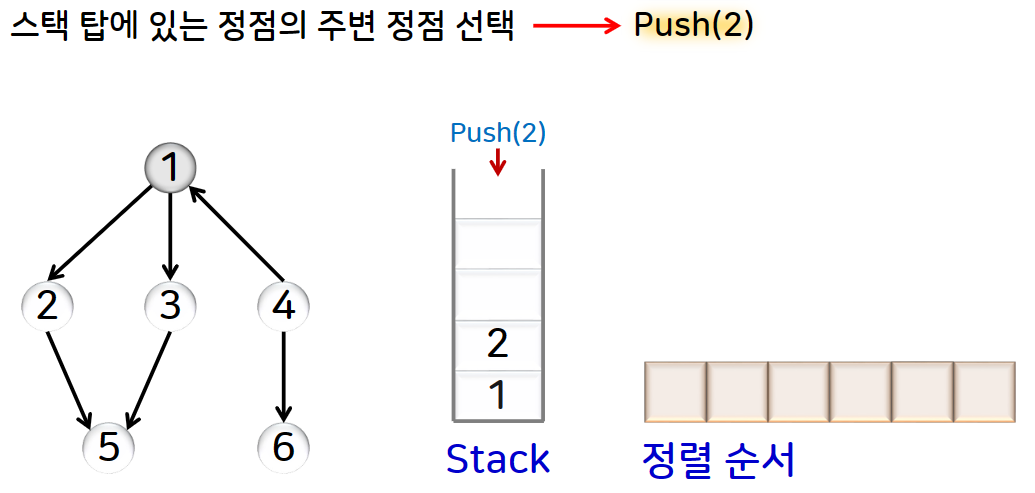




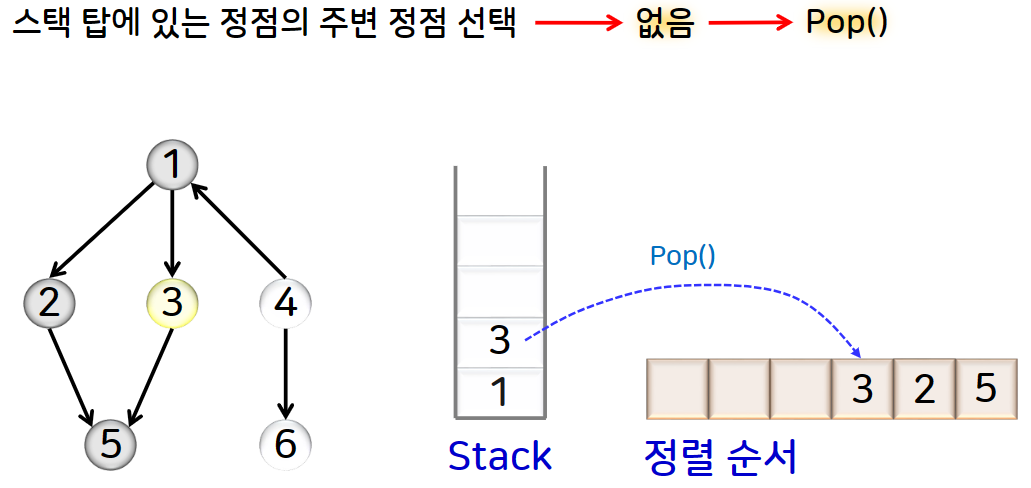



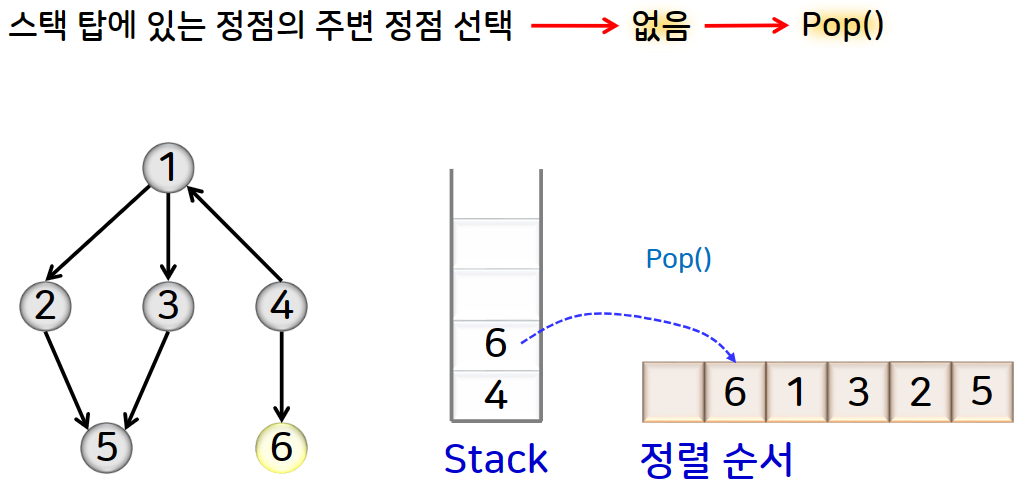
5) 그래프의 연결성
1] 연결성분
무방향 그래프에서 임의의 두 정점간의 경로가 존재하는 최대 부분 그래프입니다.
이는 너비 우선 탐색 또는 깊이 우선 탐색을 활용하여 구합니다.
while(아직 탐색하지 않은 정점이 존재)
탐색을 수행하다가 큐 또는 스택이 비게되면
그때까지 탐색한 정점들을 하나의 연결성분으로 구성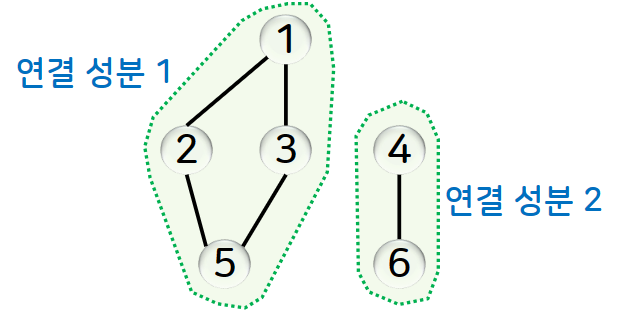
2] 강연결성분
방향 그래프에서 임의의 두 정점 사이에 양방향의 경로가 존재하는 최대 부분 그래프를 강연결성분이라고합니다.
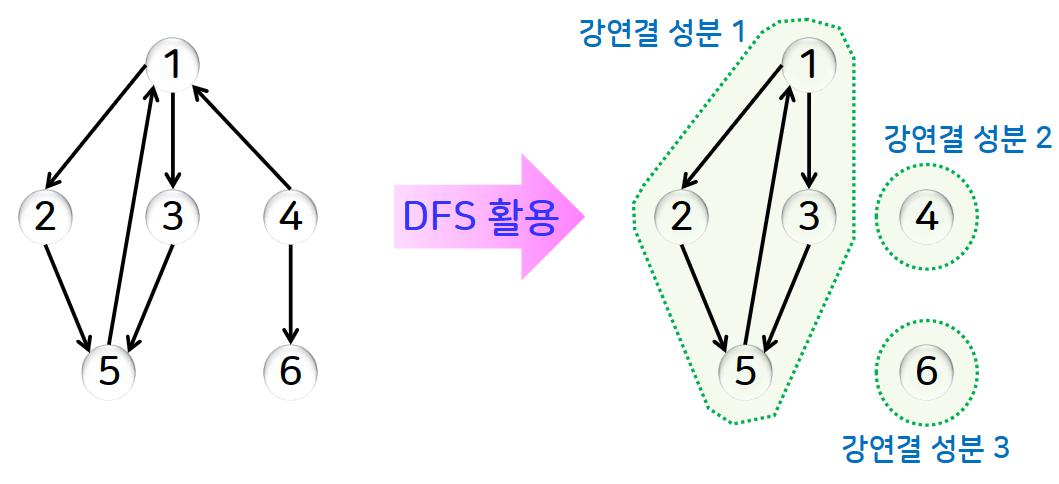
예제를 그림으로 표현하면 아래와 같습니다.


'CS(Computer Science) 이론 > 자료구조' 카테고리의 다른 글
| [자료구조] 트리 (0) | 2025.09.07 |
|---|---|
| [자료구조] 큐(QUEUE) (0) | 2025.09.07 |
| [자료구조] 스택 (0) | 2025.09.06 |
| [자료구조] 연결리스트 (0) | 2025.09.04 |
| [자료구조] 배열 (0) | 2025.08.24 |

