1. 명제
참과 거짓을 구별할 수 있는 문장이나 수학적 식을 명제라고합니다. 즉 주관적인 값이 아닌 객관적인 값이 명제가 됩니다.
명제가 타당한 경우 참 또는 T(True)라고 하고 명제가 타당하지 않은 경우 거짓 또는 F(False)라고 합니다.
2. 논리연산자
1) 논리합(or, ∨)
진리표는 아래와 같습니다.
| p | q | p ∨ q |
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
위의 진리표를 해석해보자면 p,q중 하나만 참이여도 결과는 참이 나옵니다. 즉 모두가 거짓이 아니라면 결과는 참이 됩니다.
2) 논리곱(and, ∧ )
진리표는 아래와 같습니다.
| p | q | p ∧ q |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
위의 진리표를 해석하면 p,q 모두가 참이여야 결과가 참이 됩니다. 그 외에는 모두 거짓이 됩니다.
3) 부정(~, ᄀ)
진리표는 아래와 같습니다.
| p | ~p |
| T | F |
| F | T |
4) 배타적 논리합(xor, ⊕)
p⊕q = (p ∧ ~q) ∨ (~p ∧ q) 입니다.
| p | q | p ∧ ~q | ~p ∧ q | (p ∧ ~q) ∨ (~p ∧ q) | p ⊕ q |
| T | T | F | F | F | F |
| T | F | T | F | T | T |
| F | T | F | T | T | T |
| F | F | F | F | F | F |
위의 진리표를 해석해보면 결국 두개의 값이 동일하다면 결과는 거짓이 되고 다르다면 참 됩니다.
3. 조건명제(→)
조건 명제는 화살표로 표시합니다. 예를 들면 p → q라면 명제 p가 조건이고 명제 q가 결론이 됩니다.
이럴 때 p는 q의 충분조건이라 하고 q는 p의 필요조건이라 합니다.
조건명제의 진리표는 아래와 같습니다.
| p | q | p → q |
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
위의 진리표를 해석해보면 조건이 참일때는 조건명제는 결론의 값을 따르지만 조건이 거짓일때는 결론에 상관없이 참이 됩니다.
4. 쌍조건 명제(↔)
명제 p와 q가 있을 때 명제 p와 q가 조건과 결론이 모두 되는 경우에 쌍조건 명제라고 합니다.
진리표는 아래와 같습니다
| p | q | p → q | p ← q | p ↔ q |
| T | T | T | T | T |
| T | F | F | T | F |
| F | T | T | F | F |
| F | F | T | F | T |
위의 진리표를 보면 p와 q가 동일하면 참이 되고 다르면 거짓이 됩니다. 즉 ~( p⊕q ) 과 동일합니다.
5. 논리적 동치(≡)
두 명제 p와 q가 논리적으로 동등하면 논리적 동치라고합니다. 여기서 논리적으로 동등하다는 말은 두 명제가 항상 동일한 진리값을 가진다는 의미입니다.
1) 역, 이, 대우
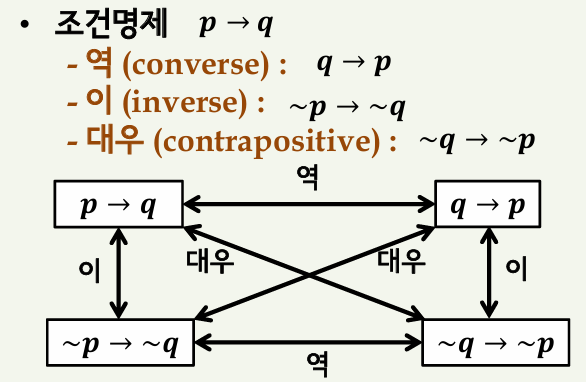
조건명제 p →q에 대해서
역은 q → p가 되고, 이는 ~p → ~q가 되며, 대우는 ~q → ~p가 됩니다.
2) 논리적 동치법칙
1] 교환법칙
p ∨ q ≡ q ∨ p
p ∧ q ≡ q ∧ p
p ↔ q ≡ q ↔ p
2] 결합법칙
(p ∨ q) ∨ r ≡ p ∨ (q ∨ r )
(p ∧ q) ∧ r ≡ p ∧ (q ∧ r )
3] 분배법칙
p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r )
p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r )
4] 항등법칙
p ∨ F ≡ p
p ∧ F ≡ p
5] 지배법칙
p ∨ T ≡ T
p ∧ F ≡ F
6] 부정법칙
~T ≡ F
~F ≡ T
p ∨ ~p ≡ T
p ∧ ~p ≡ F
7]이중 부정법칙
~(~p) ≡ p
8] 멱등법칙
p ∨ p ... ∨ p ≡ p
p ∧ p ....∧ p ≡ p
9] 드 모르간의 법칙
~(p ∨ q) ≡ (~p) ∧ (~q)
~(p ∧ q) ≡ (~p) ∨ (~q)
10] 흡수법칙
p ∨ (p ∧ q) ≡ p
p ∧ (p ∨ q) ≡ p
11] 함축법칙
p → q ≡ ~p ∨ q
12]대우법칙
p → q ≡ ~q → ~p
3) 항진명제와 모순명제
합성명제를 구성하는 명제의 진리값과 상관없이 항상 참인 명제를 항진명제라고 하고 항상 거짓인 명제를 모순명제라고 합니다.
6.술어논리와 명제함수
1) 명제함수
변수의 값에 의해 함수의 진리값이 결정되는문장이나 식을 명제함수라고 합니다.
이러한 명제함수에는 변수의 값을 적시하는 경우와 변수의 범위를 제시하는 경우가 있습니다.
후자의 경우 한정화라고 하며 기호는 ∀ 와 ∃를 사용합니다.
전자의 예시는 아래와 같습니다.
p(x,y) 가 x+y+3 = 8일때 p(1,2) 의 진리값은?
x,y에 각각 1,2를 넣으면 6 = 8은 거짓이 되므로 p(1,2)의 진리값은 F가 됩니다.
후자인 한정화에는 전체한정자와 존재한정자가 있습니다.
전체한정자는 ∀를 사용하며 명제함수 ∀xP(x)는 정의역의 모든(임의의) x에 대해서 P(x)가 참임을 의미합니다.
존재한정자는 ∃를 사용하며 명제함수 ∃xP(x)는 정의역의 어떤x에 대해서 P(x)가 참임을 의미합니다.
즉 전체한정자는 범위의 어떤값을 넣어도 항상 참이 나와야하며 존재한정자는 범위의 값 중 단 하나라도 참이 되는 값이 있다면 된다는 것입니다.
7. 타당성 검사
타당성 검사의 방법에는 벤다이어그램, 삼단논법 등이 있습니다.
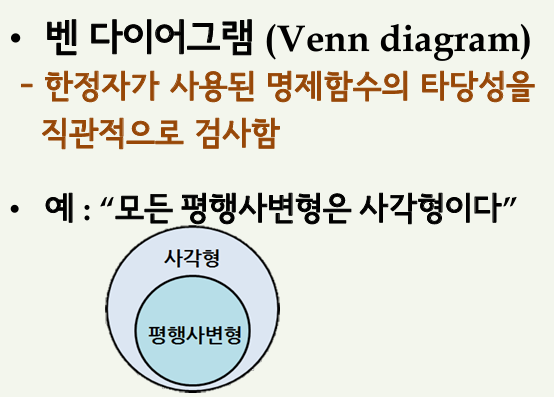
ex) 벤다이어그램
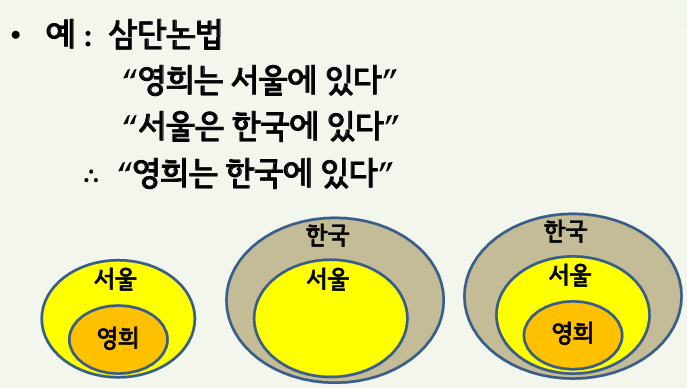
ex2) 삼단논법
8. 추론
참으로 알려진 명제를 기초로 하여 다른명제를 유도해 내는 과정을 추론이라고 합니다.
여기서 결론의 근거를 제공하는 알려진 명제를 전제라고 하며, 새로 유도된 명제는 결론이라고 합니다.
1) 유효추론
전제를 참이라고 가정했을 때 결론이 항상 참이되는 추론을 유효추론이라고 합니다.
2) 추론 규칙
선언적 부가, 단순화, 긍정논법, 부정논법, 선언적 삼단논법, 가설적 삼단논법 등이 있습니다.

'CS(Computer Science) 이론 > 이산수학' 카테고리의 다른 글
| [이산수학] 함수 (0) | 2024.05.06 |
|---|---|
| [이산수학] 관계 (2) | 2024.05.05 |
| [이산수학] 행렬 (0) | 2024.05.05 |
| [이산수학] 집합론 (1) | 2024.05.01 |
| [이산수학] 증명 (1) | 2024.04.28 |

