1. 곱집합
집합 A와 B의 곱집합 A x B는 A의 원소와 B의 원소의 모든 순서쌍들의 집합입니다.
즉 A의 원소와 B의 원소를 하나의 집합에 넣은 것입니다.
따라서 아래처럼 표현할 수 있습니다.

2. 관계

3. 관계의 표현
1) 화살표 도표

예제1)

y>x라는 것은 B의 원소가 A원소보다 큰 값의 집합을 의미합니다. 따라서 (1,2)이며 화살표 도표에서는 위처럼 표시합니다.
예제2)

이 예제도 A의 원소와 B의 원소 중 동일한 값을 찾으라는 문제이기 때문에 (1,1),(2,2)가 됩니다.
예제3)

2) 방향그래프

그래프 G = (V,E)에서 방향을 가지면 G는 방향 그래프가 되고 방향을 가지지 않으면 G는 무향그래프가 됩니다.
예제)
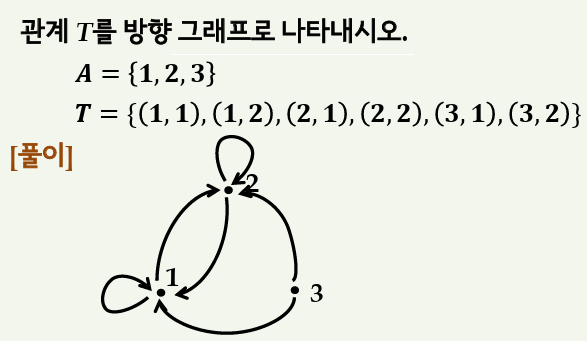
위 그래프를 해석하면 1 → 1, 1 → 2, 2 → 1, 2 → 2, 3 →1, 3 → 2 입니다. 1,2,3을 임의의 위치에 두고 방향을 그리면 됩니다.
3) 부울행렬

예제)

총 개수는 A x A = 9개입니다. 그중 T의 개수는 6개입니다.
4. 관계의 성질

반사적이라는 것은 동일한 값이 하나의 집합의 원소의 개수만큼 존재해야합니다.
예컨대 A = {1,2,3,4}라면 (1,1),(2,2),(3,3),(4,4)가 존재해야 반사적입니다.
대칭적이라는 것은 임의의 원소 a,b에 대해 (a,b)가 관계R에 존재한다면 반드시 (b,a)도 관계R에 존재해야 한다는 뜻입니다.
추이적이라는 것은 (a,b)가 관계 R에 존재하고 (b,c)가 관계 R에 존재한다면 반드시 (a,c)도 관계R에 존재해야한다는 뜻입니다.
1) 부울행렬에서의 반사적
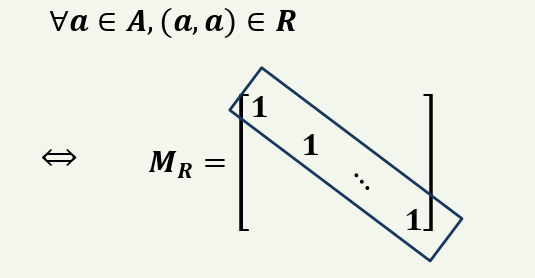
2) 부울행렬에서의 대칭적
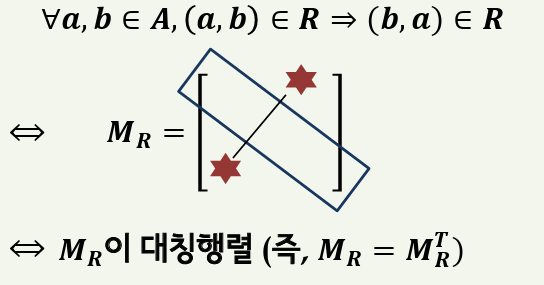
3) 부울행렬에서의 추이적
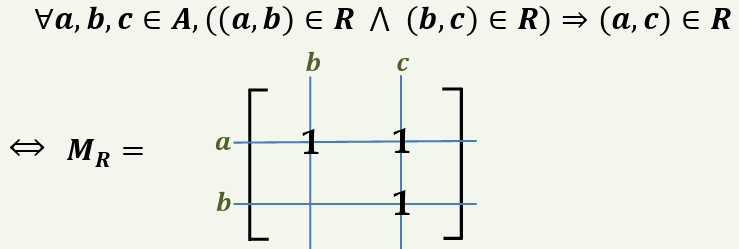
5. 관계의 종류
1) 역관계

역관계는 화살표가 반대로 향한다고 생각하시면 됩니다. 즉 주어진 그림에서의 역관계 R-1은
(a,3),(c,1),(c,4)가 됩니다.
예제) R과 S의 역관계 구하기
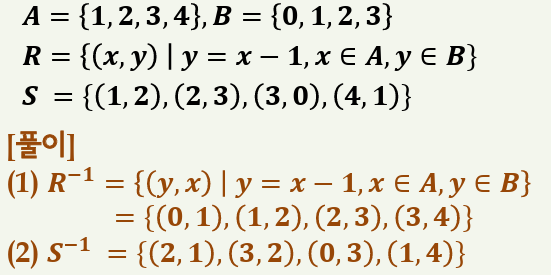
관계 R을 구하면 {(1,0),(2,1),(3,2),(4,3)이 됩니다. 역관계를 구하면 x와 y가 반대로 되므로 R-1 = {(0,1),(1,2),(2,3),(3,4)}가 됩니다.
S의 역관계 또한 x,y의 위치를 변경하면 됩니다.
2) 합성관계

합성관계는 그림으로 표현하는게 더 쉽습니다.
아래 예제를 보겠습니다.
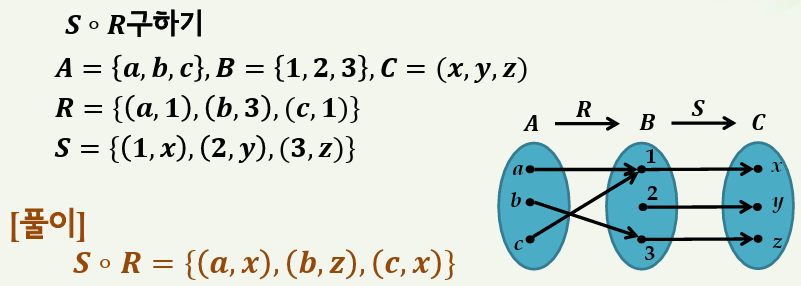
오른쪽 그림처럼 표현하면 쉽게 알 수 있습니다.
예제2)

위 예제 같은 경우에는 R에서 b = a+1 이라고 했으므로 아래 S의 b값에 a+1을 대입하면 c = a-4가 됩니다.
3) 합성관계의 부울행렬 표현

4) 동치관계


5) 동치류

예제)

'CS(Computer Science) 이론 > 이산수학' 카테고리의 다른 글
| [이산수학] 부울대수 (0) | 2024.05.09 |
|---|---|
| [이산수학] 함수 (0) | 2024.05.06 |
| [이산수학] 행렬 (0) | 2024.05.05 |
| [이산수학] 집합론 (0) | 2024.05.01 |
| [이산수학] 증명 (1) | 2024.04.28 |

