728x90
1. 기본개념
1) 논리학과 집합론

논리합(or) 이 합집합이 되며 논리곱(and)은 교집합이라고 합니다.
2) 집합과 원소
집합은 무정의 용어라고도 합니다.
즉 정의없이 사용하는 용어이며, 직관적으로 이해할 수 있으나 다른용어로 정의하기 힘든 대상을 표현하기 위해 사용됩니다.
3) 집합의 표기법
집합의 표기법은 아래와 같습니다.

4) 부분집합
위에서 a는 집합의 원소를 얘기하지만 아래에서 A는 집합을 얘기합니다.

5) 진부분집합
진부분 집합이란 A가 B에 완전히 속해있을 때 진부분집합이라고 합니다.

6) 상동
상동은 집합A와 집합B가 동일한것을 의미합니다.
표기는 아래처럼 합니다.
𝑨 =𝑩 ⇔ 𝑨⊆𝑩 𝒂𝒏𝒅 𝑩⊆𝑨
7) 서로소와 쌍으로 서로소
서로소는 집합 두개를 비교했을 때 교집합이 공집합일 경우이고, 쌍으로 서로소는 집합 3개 이상을 비교했을 때 모든 집합의 교집합이 공집합일때일 경우입니다.

8) 분할
공집합이 포함되지 않으며 부분집합도 집합이기 때문에 {}로 표기되어야합니다.

9) 멱집합

예컨대 집합 S = {a,b,c} 일대 S의 멱집합 P(S)는 아래와 같습니다.

2. 집합연산
1)합집합

2) 교집합

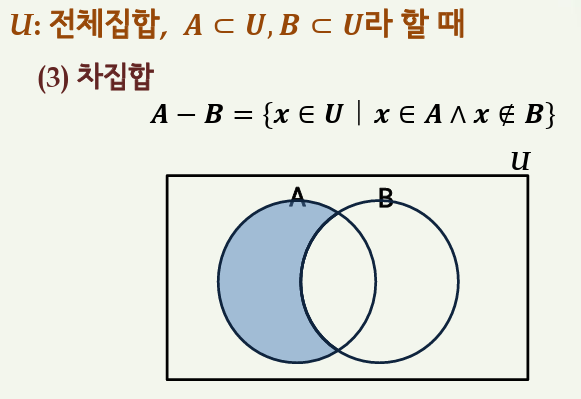
3) 차집합
4) 여집합

5) 대칭차집합

3. 집합의 대수법칙
1) 합집합의 크기


2) 서로소인 집합의 합집합의 크기

3) 교집합, 합집합, 포함관계의 이행성

4) 원소 논증

5) 집합의 항등식

6)포함관계에 대한 동치


