1. 논리게이트
1) 기본 논리게이트
1] AND 게이트

2] OR 게이트

3] NOT 게이트

2) 응용 논리게이트
1] NAND 게이트

2] NOR 게이트

3] XOR 게이트
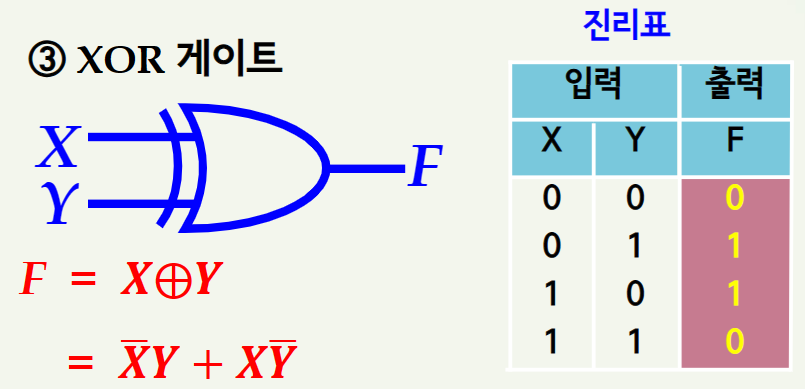
4] XNOR 게이트
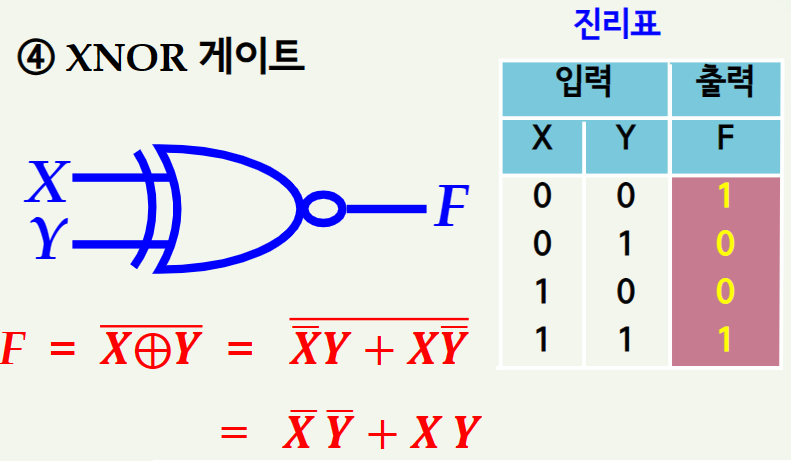
2. 부울대수
1) 부울식
부울식은 다음과 같이 순환적으로 정의합니다.

2) 부울대수의 기본정리
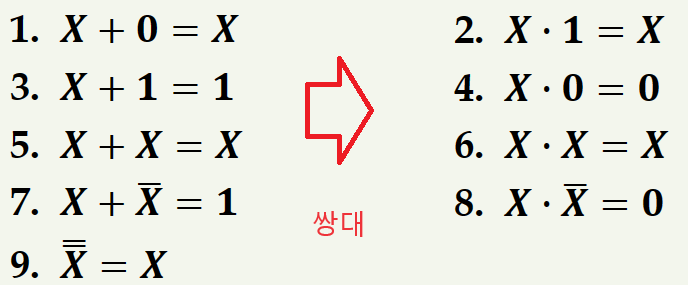

쌍대에 대한 내용은 아래에서 나옵니다.
앞선 글에서 이산수학 논리부분과도 연결되는 부분이 있습니다.
논리에 대한 글은 아래를 참고하시면 됩니다.
[이산수학] 논리
1. 명제참과 거짓을 구별할 수 있는 문장이나 수학적 식을 명제라고합니다. 즉 주관적인 값이 아닌 객관적인 값이 명제가 됩니다.명제가 타당한 경우 참 또는 T(True)라고 하고 명제가 타당하지 않
zero-week.tistory.com
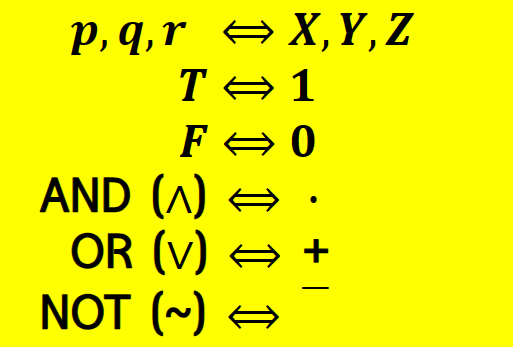
위에서 앞부분이 논리이고 뒷부분이 부울대수입니다.
이를 부울대수에 기본정리에 적용하면 아래와 같습니다.
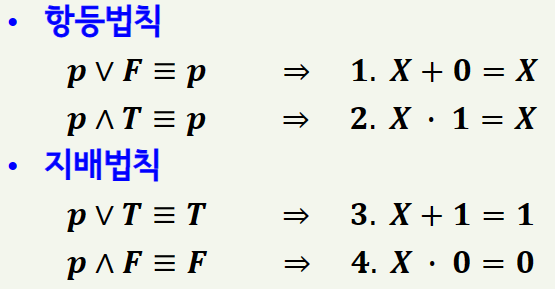

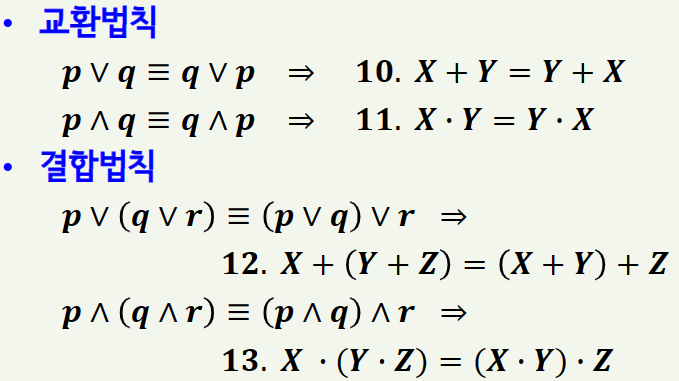
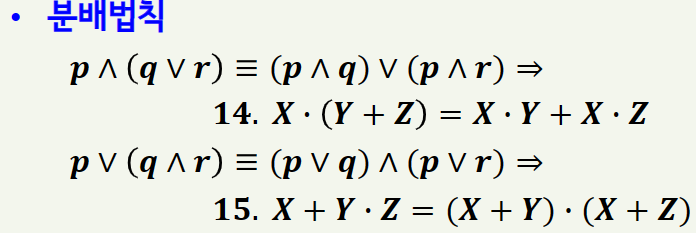
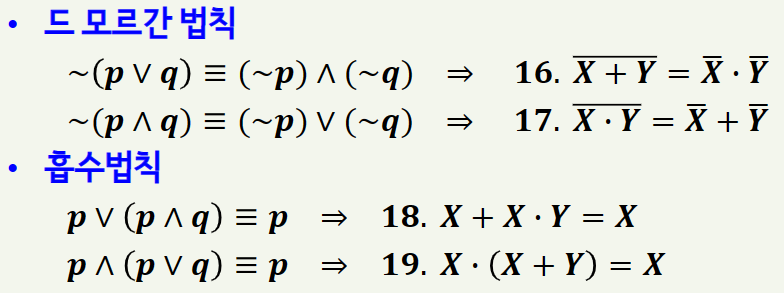
3) 쌍대성원리와 보수
부울식에서 논리곱과 논리합을 서로 바꾸고 논리상수 0과 1을 서로 바꾸면 원래 부울식의 쌍대를 얻게됩니다.
이때 주어진 부울식과 그것의 쌍대는 진리값이 서로 같다는 것이 쌍대성원리입니다.
1] 드 모르간의 일반화
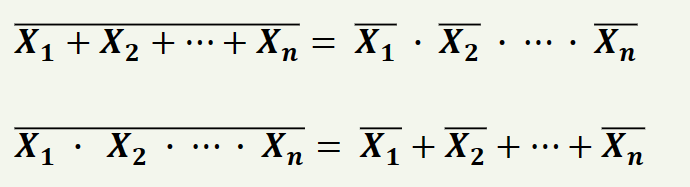
2] 보수 구하기

보수를 구할때는 아래의 두가지 방식을 이용합니다.

예제1) 드모르간의 법칙을 이용한 보수 구하
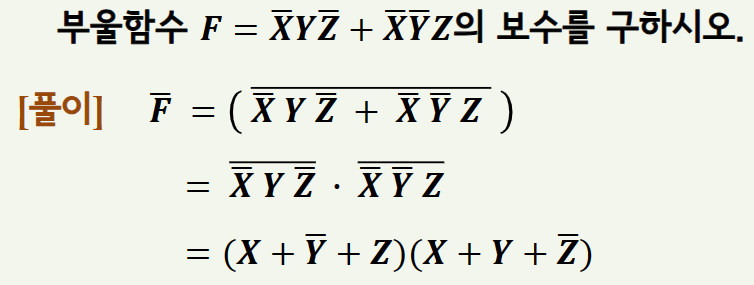
예제2) 쌍대성 원리 이용하여 보수 구하

4) 간소화
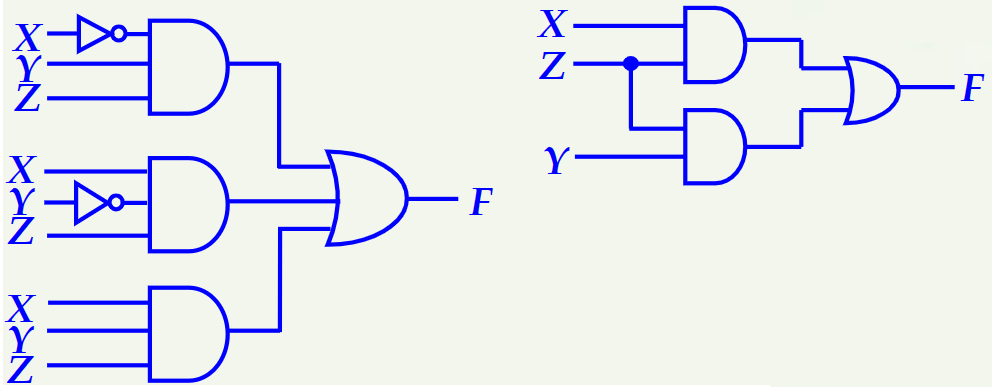
위 두가지 회로도는 같은 기능을 하는 회로도입니다. 그런데 왼쪽은 매우 복잡하고 오른쪽은 훨씬 간단한 것을 볼 수 있습니다. 즉 간소화를 하는 이유는 복잡한 회로를 간단하게 만들어서 회로를 지나갈때마다 발생하는 저항을 줄일 수 있으며 따라서 처리속도도 향상시킬 수 있기 때문입니다.
1] 항결합
항결합은 두개의 항을 결합하여 하나의 항으로 만드는 방법입니다.
예제는 아래와 같습니다.
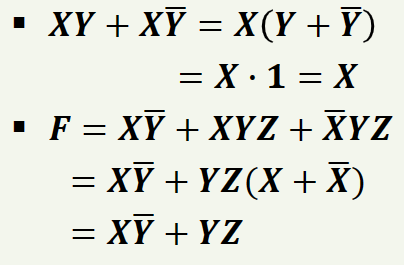
2] 문자 소거
문자소거는 중복된 문자를 제거하는 방법입니다.
예제는 아래와 같습니다.
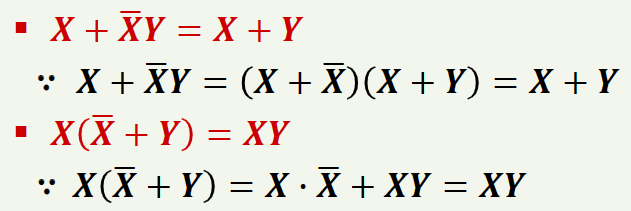
3] 중복항 첨가
부울함수의 진리값이 변하지 않도록 하면서 간소화를 위한 적절한 항을 첨가하는 방법입니다.
예제는 아래와 같습니다.
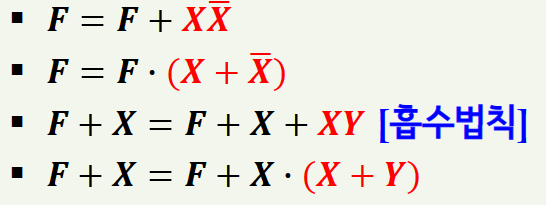
'CS(Computer Science) 이론 > 이산수학' 카테고리의 다른 글
| [이산수학] 그래프 (0) | 2024.05.22 |
|---|---|
| [이산수학] 함수 (0) | 2024.05.06 |
| [이산수학] 관계 (0) | 2024.05.05 |
| [이산수학] 행렬 (0) | 2024.05.05 |
| [이산수학] 집합론 (0) | 2024.05.01 |

