1. 주요 용어
G = (V,E) → 그래프 G는 꼭지점(V)와 변(E)들로 구성되어있다는 의미입니다.
변은 두 꼭지점을 연결하는데 이를 이산수학에서는 변에 의해 발생되었다고 표현합니다.
연결된 두 꼭지점은 서로 인접한다고 표현합니다.
벙렬변이란 두 꼭지점을 연결하는 변이 복수개 있을 때입니다.
루프란 동일한 꼭지점을 연결하는 변입니다. 즉 꼭지점(V1) 에서 꼭지점(V1)으로 갈 때입니다.
고립된 꼭지점이란 어떠한 변도 연결되지 않은 꼭지점을 의미합니다.
예제는 아래와 같습니다.

예제2)

1) 방향 그래프와 무향그래프
변이 방향을 가지고 있는 그래프를 방향 그래프라고 하며 변이 방향을 가지고 있지 않은 그래프를 무향 그래프라고합니다.

위 그림에서 좌측이 방향그래프, 우측이 무향그래프입니다.
2) 단순 그래프와 다중 그래프
루프와 병렬변을 가지지 않는 그래프를 무향그래프라고 하며 반대로 루프와 병렬변을 가지는 그래프를 다중 그래프라고 합니다.

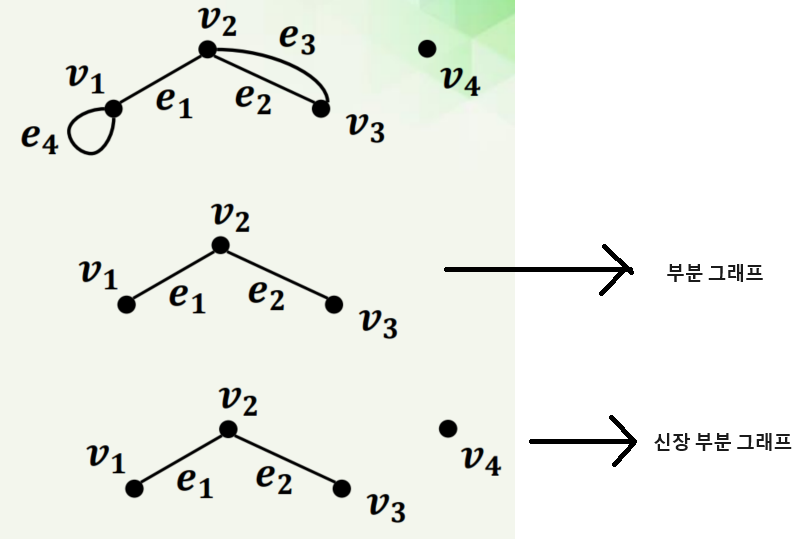
3) 부분 그래프와 신장 부분 그래프

따라서 신장 부분 그래프는 부분그래프에 속하게 됩니다.
4) 차수

예제로 확인해보면 아래와 같습니다.
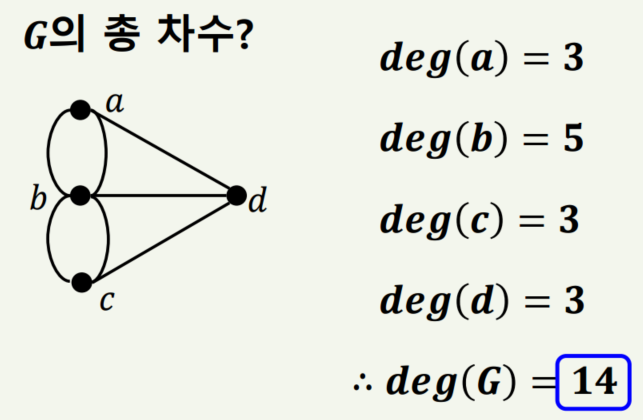
총 차수 deg(G) = deg(a)+ deg(b)+ deg(c)+ deg(d) = 3 + 5 + 3 + 3 = 14 입니다.
그래프에서 총 차수는 항상 짝수가 됩니다. 또한 변의 총 개수의 두배입니다.
5) 워크, 트레일, 경
그래프 G(V,E), v0, vk ∈ V 일때
v0부터 시작하여 vk에 도착하는 꼭지점과 변들을 순서대로 나열한 것을 워크라고 합니다.
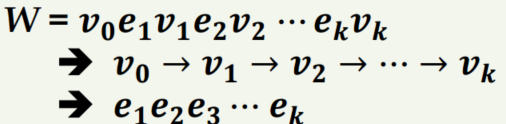
이 때 v0는 시작점, vk는 종점이라고 하며 v1,v2,...v(k-1)은 내부점이라고 합니다.
또한 k는 워크(W)의 길이라고 하며 v0 = vk일대 W는 닫혀있다고합니다.
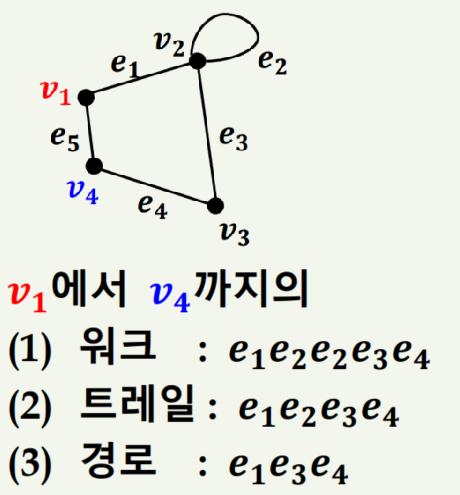
워크 W의 변들이 서로 다르면 W를 트레일(trail)이라고 합니다. 그리고 트레일 W의 꼭지점들이 모두 다르다면 W를 경로라고 합니다.
따라서 경로 ⊂ 트레일 ⊂ 워크 가 됩니다.
예제는 아래와 같습니다.
그리고 W가 트레일이고 v0 = vk이면 W는 닫힌 트레일이라고 하고 W가 경로이고 v0 = vk이면 W는 닫힌 경로라고 합니다. 특히 닫힌 경로는 사이클이라고도 하며 길이가 k인 사이클을 k-사이클이라고 합니다.
닫힌 W의 예제는 아래와 같습니다.
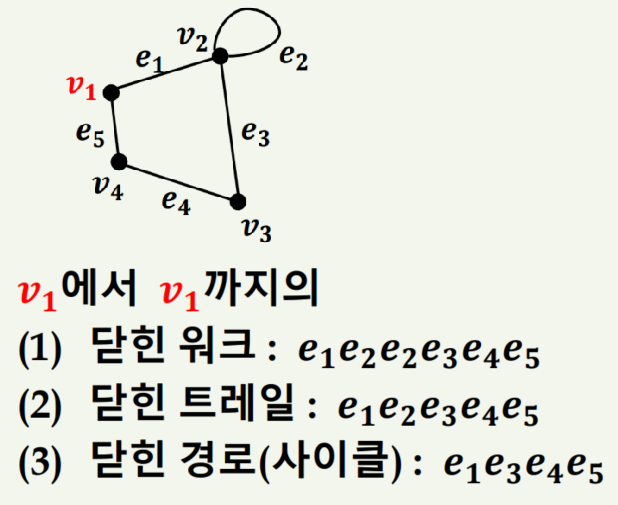
6) 연결
그래프 G(V,E), v0, u,v ∈ V 일때
u에서 v로 가는 경로가 존재하면 u와 v는 연결되어 있다고 합니다.
V의 꼭지점들은 서로 연결되고 다른 집합과 겹치지 않는 꼭지점들의 집합 V1, V2,...,Vn으로 나눌 수 있는데
이 꼭지점들의 집합을 그래프 G의 연결성분이라고 합니다.
∀u, ∀v ∈ V이고 u에서 v로 가는 경로가 존재하면 그래프 G는 연결 그래프라고 합니다. 연결 그래프는 오직 하나의 연결성분으로만 구성되어 있습니다.
예제는 아래와 같습니다.
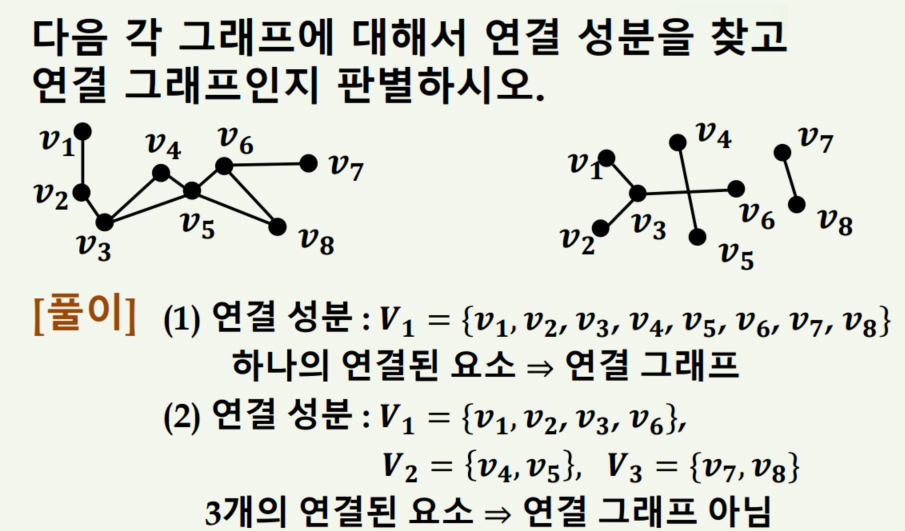
2. 그래프의 종류
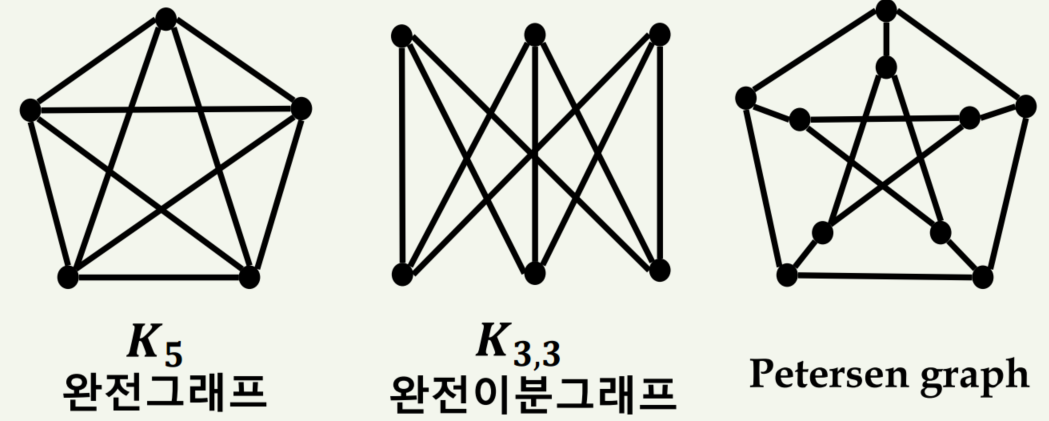
1) 완전 그래프
∀u, ∀v ∈ V 이며 ∃e = (u,v) ∈ E라면 G는 완전 그래프입니다.
표현은 K로 하며 Kn은 |V| = n인 완전 그래프를 의미합니다.
또한 완전 그래프는 임의의 두 꼭지점을 연결하는 변이 항상 존재하는 그래프입니다.
예제는 아래와 같습니다.
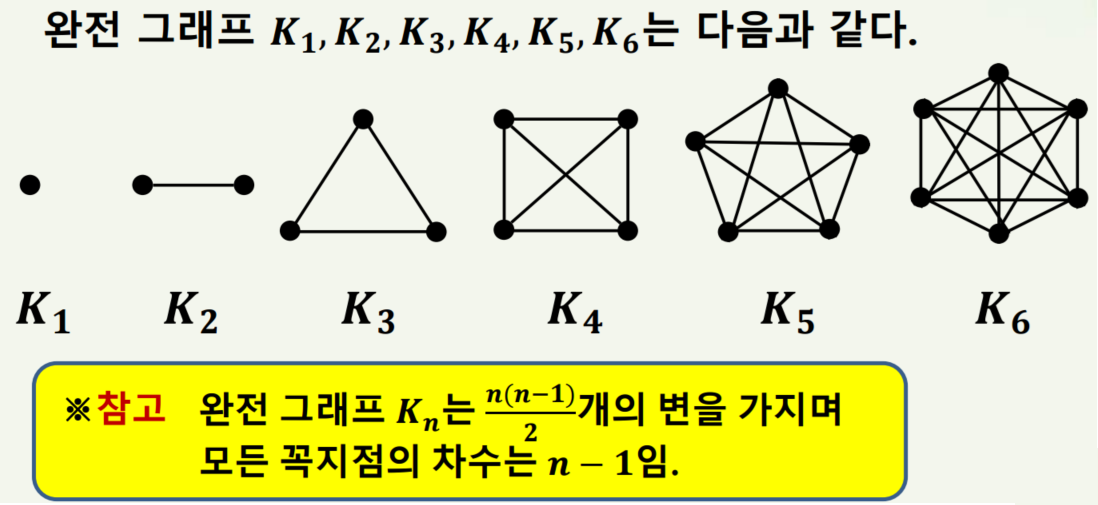
2) 이분그래프
V는 연결성분 V𝟏과 V𝟐로 분할되어 있고 모든 변들이 V𝟏의 꼭지점과 V𝟐의 꼭지점을 인접시키는 경우 그래프 G를 이분 그래프라고합니다.
이분그래프에서는 V1∪V2 = V이고 V1∩V2 = ∮(공집합)이 됩니다. 그리고 ∀e = (v1,v2) ∈ E이고 v1 ∈ V1, v2 ∈ V2가 됩니다.
예제는 아래와 같습니다.
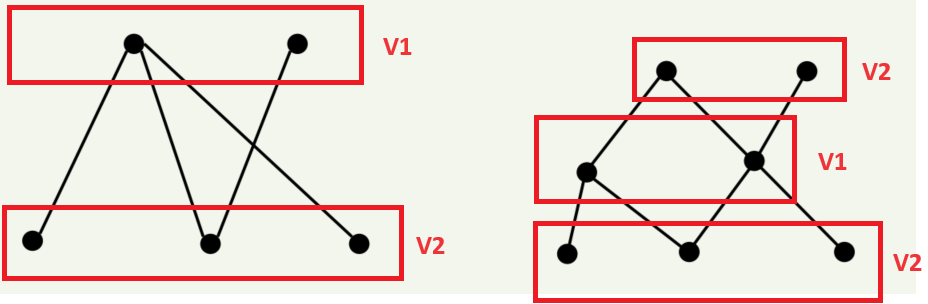
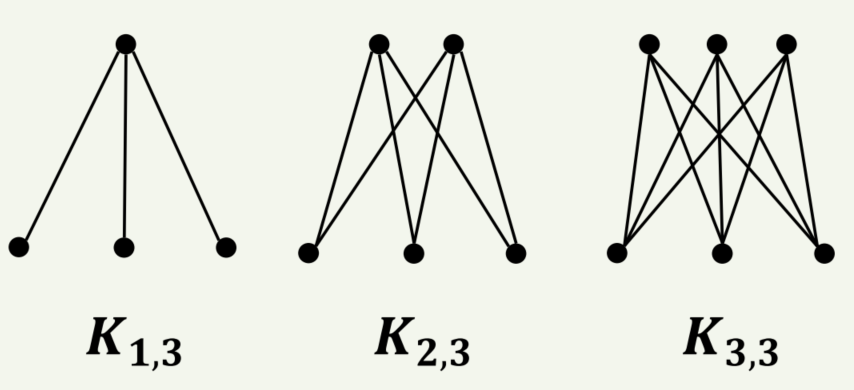
3) 완전 이분 그래프
그래프 G(V,E)가 이분 그래프이고 V1에 있는 원소하나와 V2에 있는 원소 하나를 아무거나 꺼냈을 때 그 사이에는 반드시 E가 있다는 것을 완전 이분 그래프라고 합니다.
표현은 아래처럼 합니다.
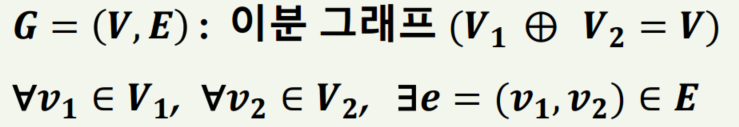
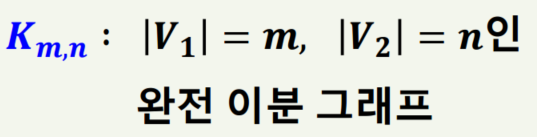
예제는 아래와 같습니다.
4) k-정규그래프
그래프 G의 모든 꼭지점들이 동일한 수의 인접한 꼭지점을 갖는 경우 G를 정규 그래프라고합니다.
이 때 정규그래프 G는 모든 꼭지점이 동일한 차수를 가집니다.
즉 ∀v ∈ V에 대하여 deg(v) = k 가 됩니다. 이 그래프를 k-정규 그래프라고 합니다.
예제는 아래와 같습니다.
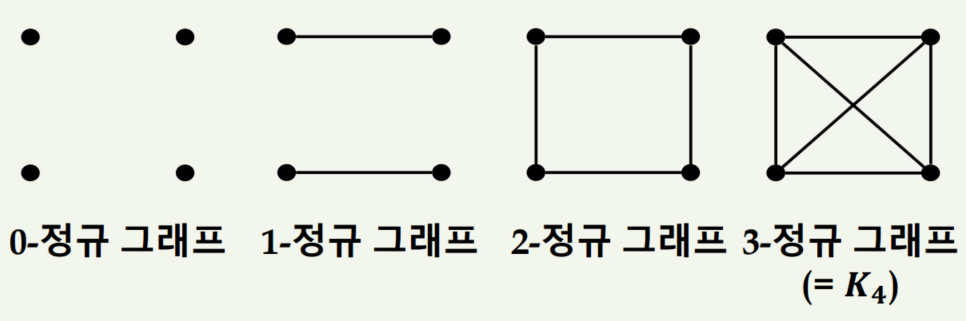
앞에서 설명한 완전 그래프는 임의의 두 꼭지점을 연결하는 변이 항상 존재하는 그래프입니다.
따라서 완전 그래프 Kn = (n-1) 정규 그래프와 동일합니다. 이 때 n은 꼭지점의 개수입니다.
3. 그래프의 표현
1) 발생행렬
그래프 G가 있을 때 꼭지점을 행으로 변을 열로 하여 변과 꼭지점 사이의 발생관계를 표현한 행렬을 발생행렬이라고 합니다. 이 때 발생행렬은 |V| x |E| 크기의 부울행렬이며 vi가 ej에 의해 발생되는 경우 aij=1이 되며 그밖의 경우 aij=0이 됩니다.
예제를 통해 자세히 확인해 보겠습니다.
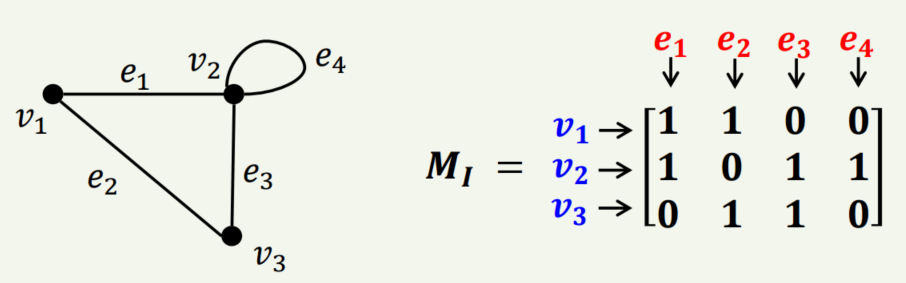
위 예제는 그래프를 발생행렬로 표현한 것입니다. v1는 e1과 e2에 의해서만 발생했기 때문에 a11 = a12 = 1이 됩니다.
한번 더 보자면 e3는 v3과 v2에 발생했다고 할 수 있으므로 a23 = a33 =1이 됩니다.
2) 인접행렬
꼭지점을 행과 열로 하여 꼭지점과 꼭지점 사이의 인접관계를 표현한 행렬을 인접행렬이라고 합니다.
인접행렬은 |V| x |V|인 정방행렬이 되며 aij = vi에서 vj로의 연결 개수를 의미합니다.
예제는 아래와 같습니다.
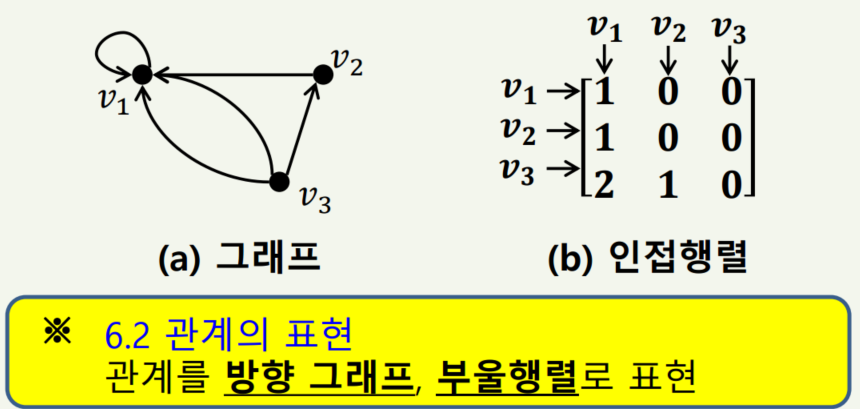
방향 그래프이기 때문에 방향도 중요합니다. 따라서 v1에서 v1으로 가는 값이 1개 있기 때문에 a11 = 1이 되고 v3에서 v1으로 가는 값이 2개이기 때문에 a31 = 2가 됩니다.
3) 인접리스트
각 꼭지점에 인접하는 꼭지점들을 차례로 연결 리스트로 표현한 것을 인접리스트라고 합니다.
예제는 아래와 같습니다.
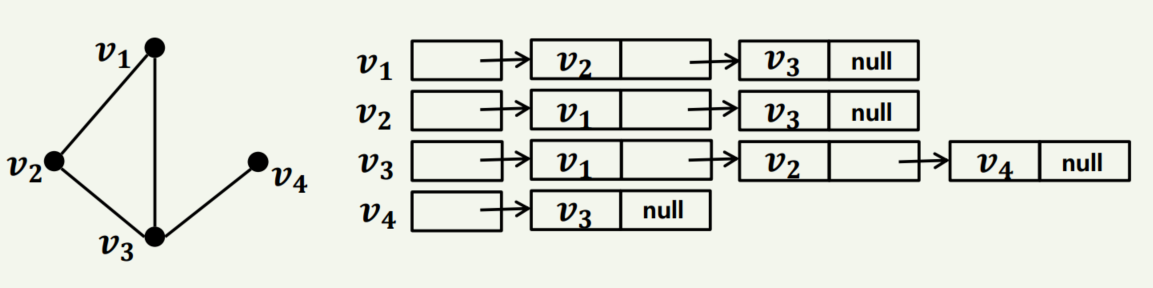
v1에서는 v2와 v3와 인접하기 때문에 v1 v2 v3 null로 표현합니다. null은 값이 없다는 것을 의미하는데 여기서는 리스트가 종료되었다고도 볼 수 있습니다.
4. 그래프의 탐색
1) 평면그래프
평면그래프란 그래프의 모든 변을 서로 교차하지 않게 그릴 수 있는 그래프입니다.
위와 같은 그래프는 평면그래프가 아닙니다.
반대로 아래와 같은 그래프는 평면 그래프입니다.
2) 오일러공식
먼저 면이 무엇인지 알아야합니다. 그래프에서 면이란 연결된 평면그래프에서 변들로 만들어지는 사이클을 경계로 형성된 공간을 의미합니다.
오일러 공식이란 연결된 평면그래프에서 꼭지점의 수를 v, 변의 수를 e, 면의 수를 f라고 하면
v - e + f = 2가 된다는 것입니다.
3) 4색정리
지도의 인접한 구역을 서로 다른색으로 칠하는데 오직 4가지 색이면 충분하다는 것이 4색정리입니다.
이를 그래프에서 표현한다면 평면 그래프가 주어졌을 때, 각 꼭지점에 대하여 인접한 꼭지점과 서로 다른 색으로 칠하는데
필요한 색은 4가지이면 충분하다는 것입니다.
4) 오일러투어
오일러 투어를 알기위해서는 오일러 트레일이란 개념을알아야합니다. 오일러 트레일이란 그래프의 모든 변들을 각각 한번만 지나는 트레일입니다.
오일러투어는 닫힌 오일러트레일입니다. 즉, 시작점과 종점이 같은 오일러 트레일이라고 할 수 있습니다.
투어라는 것은 그래프의 모든 변들이 포함된 닫힌 워크입니다.
5) 오일러 그래프 정리
1] 연결 그래프가 오일러 투어를 가지기 위한 필요충분 조건은 그래프의 모든 꼭지점의 차수는 짝수인것입니다.
증명)
연결 그래프 𝑮 = (𝑽, 𝑬)가 오일러 투어를 가진다고 가정합니다. 𝑽의 임의의 꼭지점 𝒗는 다른 꼭지점들과 변에 의해 연결됩니다. 𝒗와 연결된 변은 오일러 투어에 의해 𝒗로 들어오는 변과 나가는 변으로 구분할 수 있고, 들어오는 변의 수와 나가는 변의 수는 항상 동일합니다. 따라서 모든 꼭지점의 차수는 짝수가 됩니다.
2] 연결 그래프 𝑮의 모든 꼭지점의 차수는 짝수이면 𝑮는 오일러 그래프입니다.
증명)
그래프 𝑮가 연결 그래프이고 모든 꼭지점의 차수는 짝수라 가정합니다. 오일러 투어는 다음 알고리즘을 통해 구할 수 있습니다.
단계1 𝑮의 임의의 꼭지점 𝒗를 고릅니다.
• 단계2 𝒗에서 시작하고 𝒗에서 끝나는 임의의 사이클 𝑪을 선택합니다.
• 단계3 𝑪가 오일러 투어이면 증명을 끝냅니다.
만약 아니라면 아래 과정을 반복합니다.
• 단계3-1 𝑮에서 𝑪에 속하는 모든 변을 제거하고 새로운 𝑮′을 만듭니다.
• 단계3-2 𝑪와 𝑮′가 공유하는 꼭지점 중 하나를 고르고 𝒘라 합니다.
• 단계3-3 𝒘에서 시작하고 𝒘에서 끝나는 임의의 사이클 𝑪′을 선택합니다.
• 단계3-4 기존의 𝑪와 새로 선택된 𝑪′을 합쳐서 새로운 𝑪를 만듭니다.
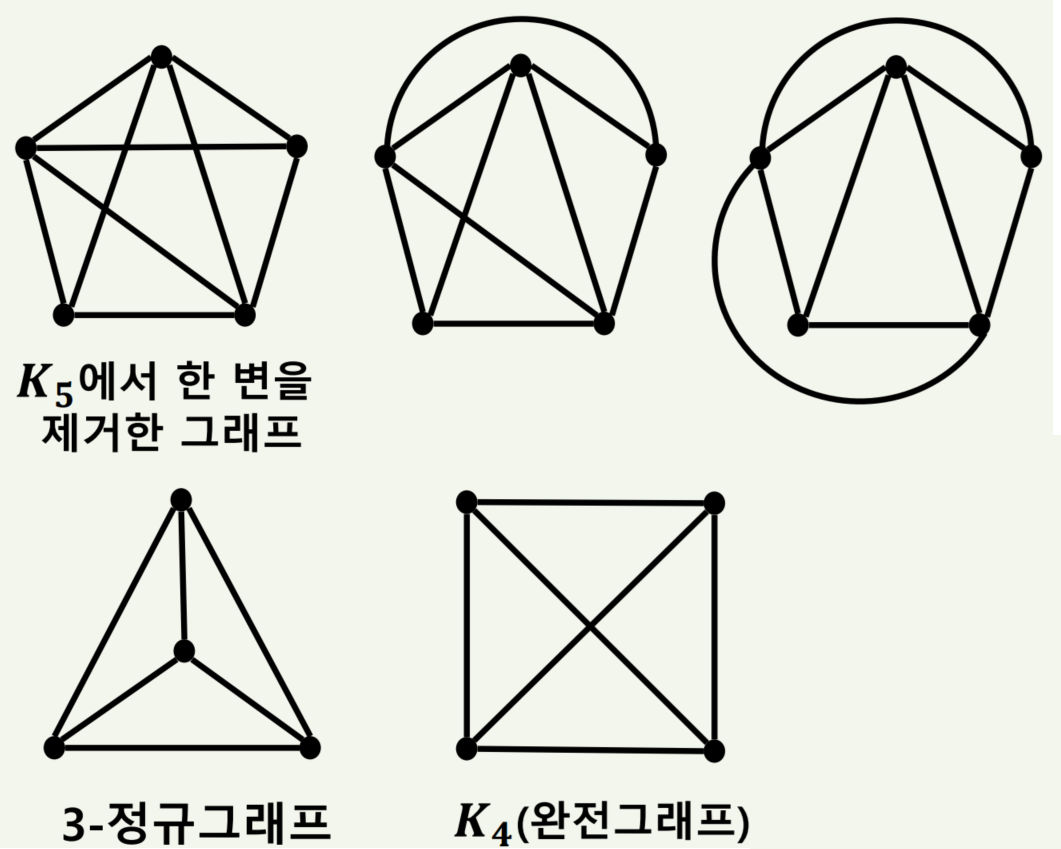
위 그림에서 오일러투어는 dabcfghe가 됩니다. 물론 다른 답안도 존재합니다.
6) 해밀턴 경로와 해밀턴 사이클
해밀턴 경로란 그래프의 모든 꼭지점들을 한 번씩만 지나는 경로를 의미하며 해밀턴 사이클이란 닫힌 해밀턴 경로입니다.
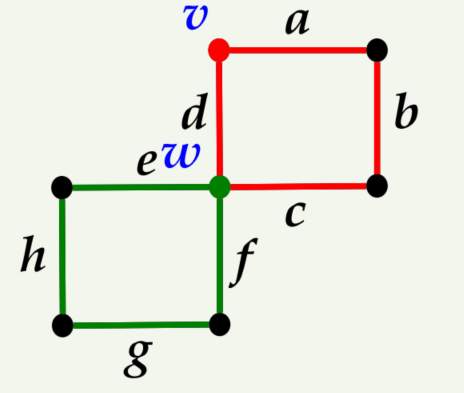
좌측의 이동방향은 abcdh가 됩니다. 이렇게하면 모든 꼭지점은 지나지만 시작점과 종점이 다르기 때문에 해밀턴 경로는 맞지만 해밀턴 사이클은 아닙니다.
우측의 이동방향은 abekl입니다. 그런데 변 i를 이으면 시작점과 종점이 같아집니다. 따라서 우측은 해밀턴 사이클이 됩니다.
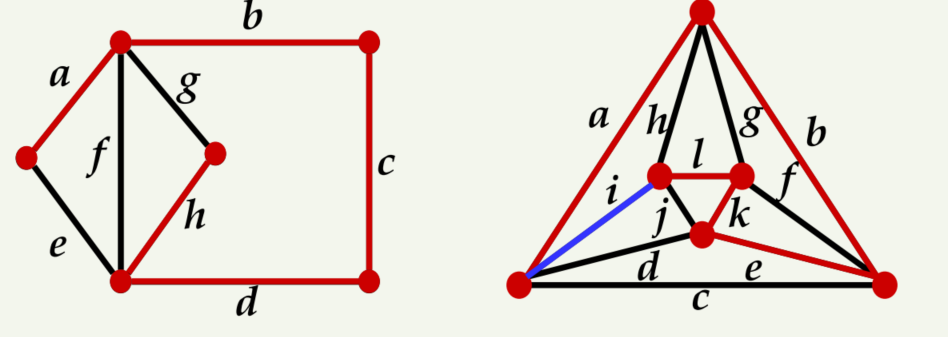
이것 경로만 잇는 그림으로 표현하면 아래와 같습니다.
5. 그래프의 활용
가중 그래프란 그래프의 각 변에 실수값이 붙여진 그래프입니다. 이 때 변의 부여된 값은 가중치라고 합니다.
이러한 가중 그래프를 이용하여 최단경로 문제, 최소신장트리 문제 등을 계산할 수 있습니다.
최단 경로 문제는 출발지와 도착지가 주어졌을 때 가장 짧은 경로를 찾는 문제이고, 최소 신장 트리 문제는 그래프의 모든 꼭지점을 최소 수의 변으로 연결하는 문제입니다.
최단 경로 문제의 대표적인 알고리즘은 데이크스트라 알고리즘이 있습니다.
데이크 스트라 알고리즘의 계산방법은 아래 페이지를 참고하시면 됩니다.
[알고리즘] 그래프 알고리즘
1. 최소 신장 트리1) 정의신장트리란 가중 무방향 그래프에서 모든 정점을 포함하는 트리를 의미합니다. 즉 정점이 n개라면 트리에는 n-1개의 간선이 존재합니다. 이 중 최소(비용) 신장 트리는
zero-week.tistory.com
'CS(Computer Science) 이론 > 이산수학' 카테고리의 다른 글
| [이산수학] 부울대수 (0) | 2024.05.09 |
|---|---|
| [이산수학] 함수 (0) | 2024.05.06 |
| [이산수학] 관계 (0) | 2024.05.05 |
| [이산수학] 행렬 (0) | 2024.05.05 |
| [이산수학] 집합론 (0) | 2024.05.01 |

